Đề toán 2022 Có bao nhiêu giá trị nguyên âm của tham số (a) để hàm số (y = left| {{x^4} + a.{x^2} – 8x} right|) có đúng ba điểm cực trị?
A. (5). B. (6). C. (11). D. (10).
Lời giải
Đặt (fleft( x right) = {x^4} + a{x^2} – 8x Rightarrow f'(x) = 4{x^3} + 2ax – 8.)
(f'(x) = 0 Leftrightarrow 4{x^3} + 2ax – 8 = 0 Leftrightarrow a = frac{{4 – 2{x^3}}}{x} = g(x)) (vì (x = 0) không phải là nghiệm)
(f(x) = 0 Leftrightarrow xleft( {{x^3} + ax – 8} right) = 0 Leftrightarrow left[ begin{array}{l}x = 0\a = frac{{8 – {x^3}}}{x} = h(x)end{array} right.) (vì (x = 0) không phải là nghiệm)
Ta có (g'(x) = frac{{ – 4{x^3} – 4}}{{{x^2}}};,h(x) = frac{{ – 2{x^3} – 8}}{{{x^2}}}).
adsense
Bảng biến thiên của (g(x):)
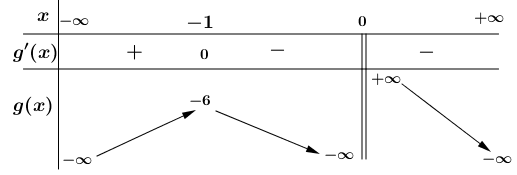
Bảng biến thiên của (h(x)):
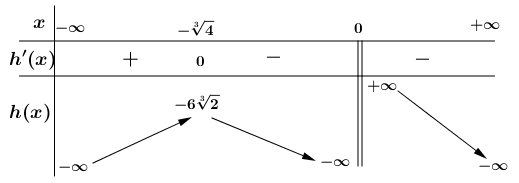
Ta thấy:
Nếu (a < – 6) thì (fleft( x right)) có 3 điểm cực trị và (f(x) = 0) có ít nhất hai nghiệm đơn nên (y = left| {f(x)} right|) có ít nhất 5 điểm cực trị.
Nếu (a ge – 6) thì (fleft( x right)) có 1 điểm cực trị và (f(x) = 0) có đúng hai nghiệm đơn nên (y = left| {f(x)} right|) có đúng 3 điểm cực trị.
Như vậy (y = left| {f(x)} right|) có đúng 3 điểm cực trị ( Leftrightarrow a ge – 6).
Có thể bạn quan tâm
- Vận may của Song Ngư trong năm 2023 sẽ ra sao?
- H2R 2023 giá bao nhiêu?
- Ca dao bao nhiêu…bấy nhiêu
- 1 gói cà phê phố bao nhiêu cafein?
- Ngày 13 tháng 5 năm 2023 là bao xa?
Vì (a) nguyên âm nên (a in left{ { – 6; – 5; – 4; – 3; – 2; – 1} right}). Do đó có 6 giá trị (a) thỏa mãn yêu cầu bài toán.
Câu hỏi: Có bao nhiêu giá trị nguyên âm của tham số $m$ để hàm số $y=dfrac{x+4}{2x-m}$ nghịch biến trên $left( -3;4 right).$
A. $2$.
B. $1$.
C. $3$.
D. vô số.
Lời giải
$y=dfrac{x+4}{2x-m}$
Điều kiện: $mne 2xLeftrightarrow xne dfrac{m}{2}$.
$y=dfrac{x+4}{2x-m}Rightarrow y’=dfrac{-m-8}{{{left( 2x-m right)}^{2}}}$
Hàm số nghịch biến trên $left( -3;4 right)$
$Leftrightarrow y'<0,forall xin left( -3;4 right)$
$Leftrightarrow left{ begin{aligned}
& -m-8<0 \
& dfrac{m}{2}notin left( -3;4 right)Leftrightarrow min left( -6;8 right) \
end{aligned} right.Leftrightarrow left{ begin{aligned}
& m>-8 \
& left[ begin{aligned}
& mge 8 \
& mle -6 \
end{aligned} right. \
end{aligned} right.Leftrightarrow left[ begin{aligned}
& mge 8 \
& -8end{aligned} right.$.
Mà $m$ nguyên âm nên $min left{ -6;-7 right}$.
Vậy có 2 giá trị nguyên âm $m$.
Đáp án A.
Click để xem thêm…
T
Written by
The Knowledge
Moderator
Moderator
- Bài viết54,433
- Điểm tương tác36
- Điểm48
( Leftrightarrow left{ begin{array}{l} – m – 8 < 0\frac{m}{2} notin left( { – 3;4} right) Leftrightarrow m in left( { – 6;8} right)end{array} right. Leftrightarrow left{ begin{array}{l}m > – 8\left[ begin{array}{l}m ge 8\m le – 6end{array} right.end{array} right. Leftrightarrow left[ begin{array}{l}m ge 8\ – 8 < m le – 6end{array} right.).
Toán
Số các giá trị nguyên âm của tham số m để tập xác định của hàm số y= $frac{2}{x-2m}$ + $sqrt[2]{7m+1-2x}$ chứa đoạn [-1;1] là: A.0 B.Vô số C.2 D.1
28/07/2021

By Jasmine
Số các giá trị nguyên âm của tham số m để tập xác định của hàm số y= $frac{2}{x-2m}$ + $sqrt[2]{7m+1-2x}$ chứa đoạn [-1;1] là:
A.0
B.Vô số
C.2
D.1
ĐK: (left{ begin{array}{l}x – 2m ne 0\7m + 1 – 2x ge 0end{array} right. Leftrightarrow left{ begin{array}{l}x ne 2m\x le dfrac{{7m + 1}}{2}end{array} right.)
( Rightarrow TXD:D = left( { – infty ;dfrac{{7m + 1}}{2}} right]backslash left{ {2m} right})
Để TXĐ chứa đoạn (left[ { – 1;1} right]) nên (left[ { – 1;1} right] subset D Leftrightarrow left{ begin{array}{l}left[ { – 1;1} right] subset left( { – infty ;dfrac{{7m + 1}}{2}} right]\2m notin left[ { – 1;1} right]end{array} right.)
( Leftrightarrow left{ begin{array}{l}1 le dfrac{{7m + 1}}{2}\left[ begin{array}{l}2m > 1\2m < – 1end{array} right.end{array} right. Leftrightarrow left{ begin{array}{l}2 le 7m + 1\left[ begin{array}{l}m > dfrac{1}{2}\m < – dfrac{1}{2}end{array} right.end{array} right. Leftrightarrow left{ begin{array}{l}m ge dfrac{1}{7}\left[ begin{array}{l}m > dfrac{1}{2}\m < – dfrac{1}{2}end{array} right.end{array} right. Leftrightarrow m > dfrac{1}{2})