Cho 2 đường thẳng cắt nhau d và d có bao nhiêu phép đối xứng trục biến d thành d

Cho hai đường thẳng d và d’cắt nhau. Có bao nhiêu phép đối xứng trục biến đường thẳng (d) thành đường thẳng (d’) :

A. Có duy nhất một phép đối xứng trục

B. Có 2 phép đối xứng trục.

C. Có vô số phép đối xứng trục

D. Không có phép đối xứng trục nào

Cho hai đường thẳng d và d’ cắt nhau. Có bao nhiêu…

Câu hỏi: Cho hai đường thẳng d và d’ cắt nhau. Có bao nhiêu phép đối xứng trục biến đường thẳng d thành đường thẳng d’:

A. Không có phép đối xứng trục nào         

B. Có duy nhất một phép đối xứng trục

C. Chỉ có hai phép đối xứng trục

D. Có rất nhiều phép đối xứng trục

Đáp án

C

– Hướng dẫn giải

Đáp án C

Khi 2 đường thẳng d và d’ cắt nhau thì có 2 phép đối xứng trục biến d thành d’.

Trục đối xứng là  2 đường phân giác tạo bởi 2 đường  thẳng đã cho

Câu hỏi trên thuộc đề trắc nghiệm

100 câu trắc nghiệm Phép dời hình cơ bản !!

Lớp 11 Toán học Lớp 11 – Toán học

Cho hai đường thẳng (d) và (d’) cắt nhau. Có bao nhiêu phép đối xứng qua mặt phẳng biến (d) thành (d’)?                

Có thể bạn quan tâm

• Rượu Chivas 18 750ml giá bao nhiêu?
• Kỳ nghỉ học năm 2023 Bihar kéo dài bao lâu
• 100g da heo luộc bao nhiêu calo?
• Chân dài bao nhiêu là đẹp
• 1 pallet nhựa nặng bao nhiêu kg

A.

 1.

B.

 2.

C.

 0.

D.

 Vô số.

Đáp án và lời giải

Đáp án:B

Lời giải:

 @ Lời giải tự luận: Giả sử (d) và (d’) cắt nhau tại I, suy ra mặt phẳng đối xứng (P) phải đi qua I. Với điểm

ta có: Đ(P)(M) =   ⇒ (P) là mặt phẳng trung trực của MM’ ⇒ ΔIMM’ là tam giác cân ⇒ IH là tia phân giác của   Tức (P) là mặt phẳng qua I, vuông góc với mặt phẳng ((d), (d’)) và chứa tia phân giác của góc tạo bởi (d) và (d’) (có hai tia phân giác). Vậy, có đúng hai phép đối xứng qua mặt phẳng biến (d) thành (d’).

Vậy đáp án đúng là B.

Câu hỏi thuộc đề thi sau. Bạn có muốn thi thử?

Bài tập trắc nghiệm 60 phút Khái niệm về khối đa diện và hình đa diện – Toán Học 12 – Đề số 5

Làm bài

Chia sẻ

Một số câu hỏi khác cùng bài thi.

• Cho hình vuông

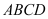   và 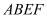 có cạnh bằng 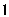, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi  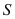là điểm đối xứng của 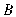qua đường thẳng 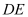. Thể tích của khối đa diện  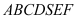bằng

• Cho khối chóp

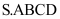  có đáy là hình bình hành, gọi 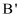và 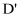 theo thứ tự là trung điểm các cạnh SB, SD. Mặt phẳng 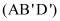cắt cạnh SC tại C’. Tính tỷ số thể tích của hai khối đa diện được chia ra bởi mặt phẳng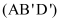         

• Trong các mệnh đề sau, mệnh đề nào sai?        

• Hình bát diện đều thuộc loại khối đa diện đều nào sau đây?  

• Cho khối lăng trụ 

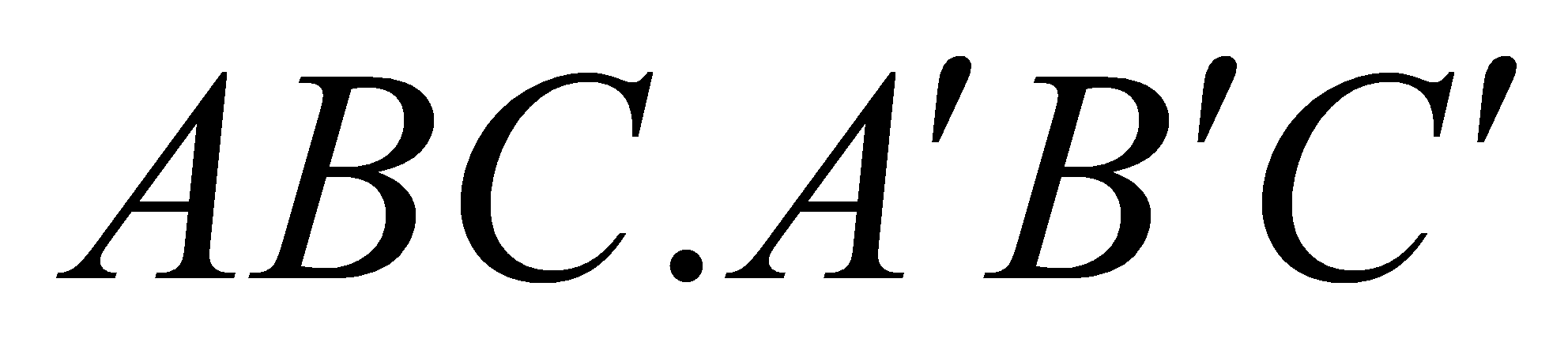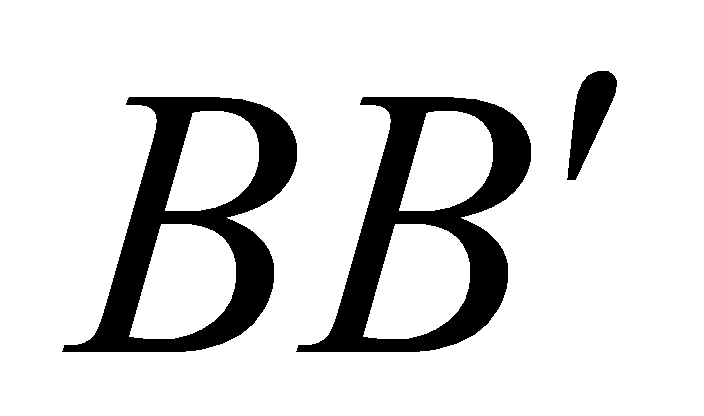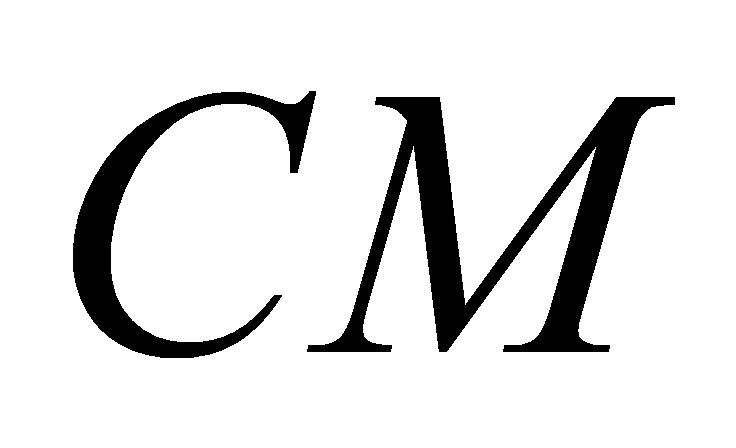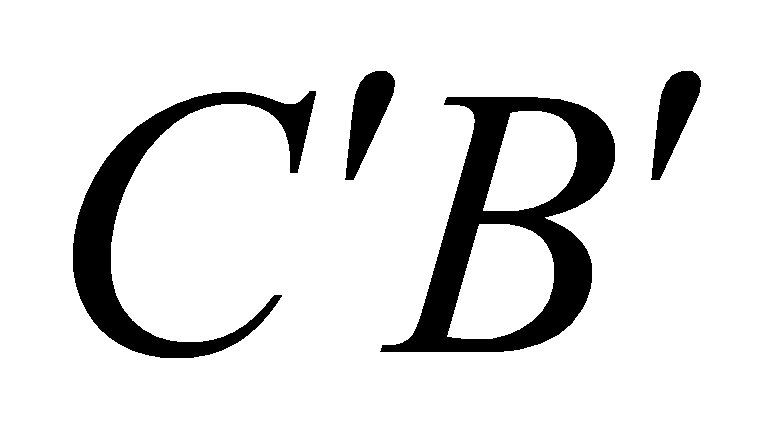   có thể tích bằng . Gọi ,  lần lượt là trung điểm của các đoạn thẳng  và . Đường thẳng  cắt đường thẳng  tại , đường thẳng  cắt đường thẳng  tại . Thể tích khối đa diện lồi  bằng

• Cho tứ diện ABCD có tam giác BCD vuông tại C, AB vuông góc với mặt phẳng (BCD),AB = 5a, BC = 3a và CD = 4a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD .  

• Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt?  

• Cho khối hộp

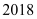   có thể tích bằng . Gọi 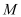 là trung điểm của cạnh 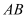. Mặt phẳng  chia khối chóp  thành hai khối đa diện. Tính thể tích phần khối đa diện chứa đỉnh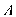         

• Cho khối chóp

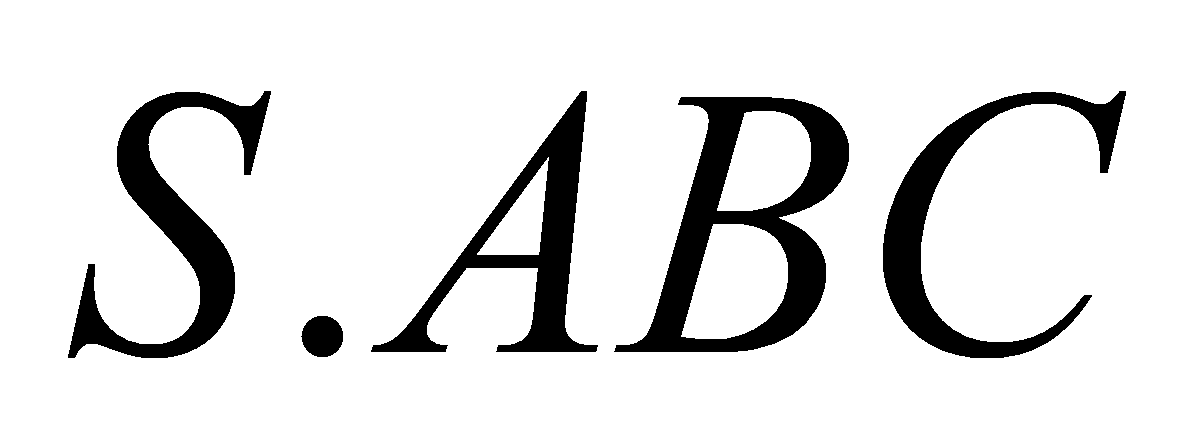  có , sao cho 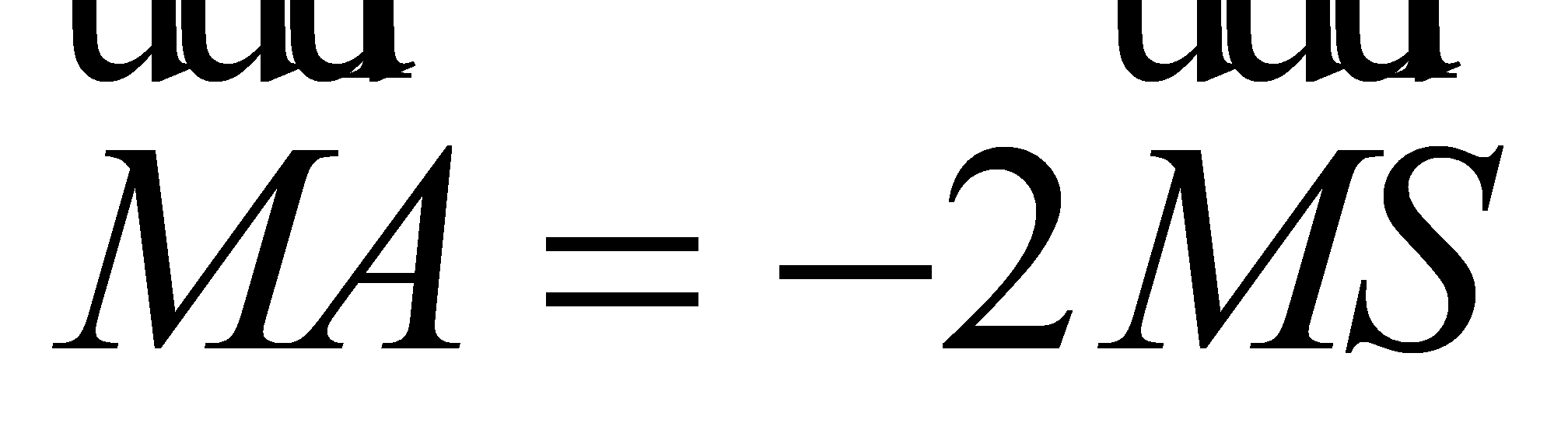, 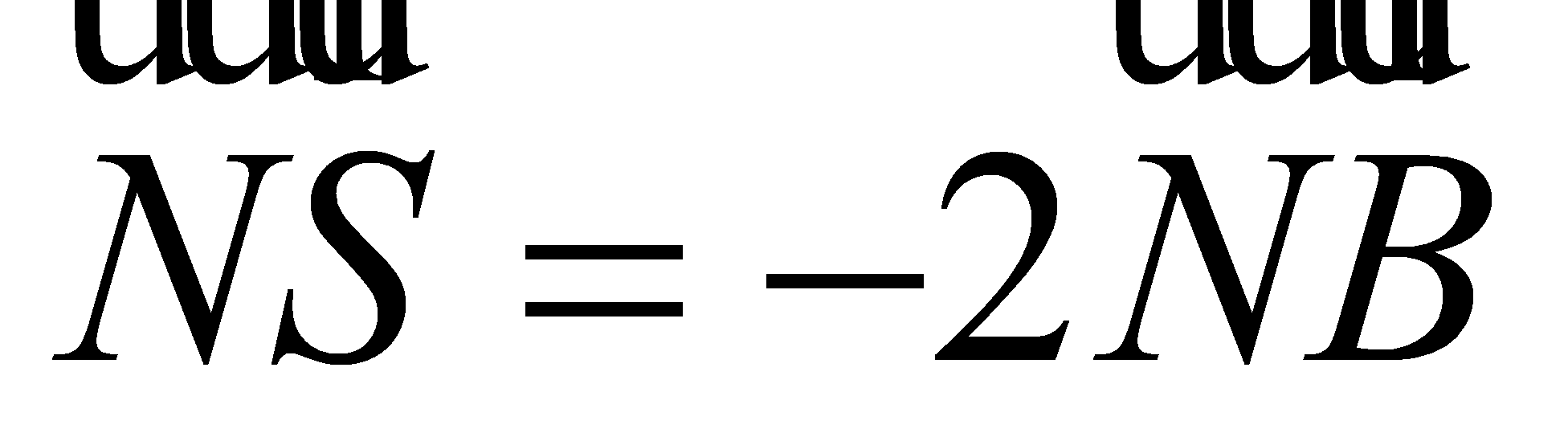. Mặt phẳng 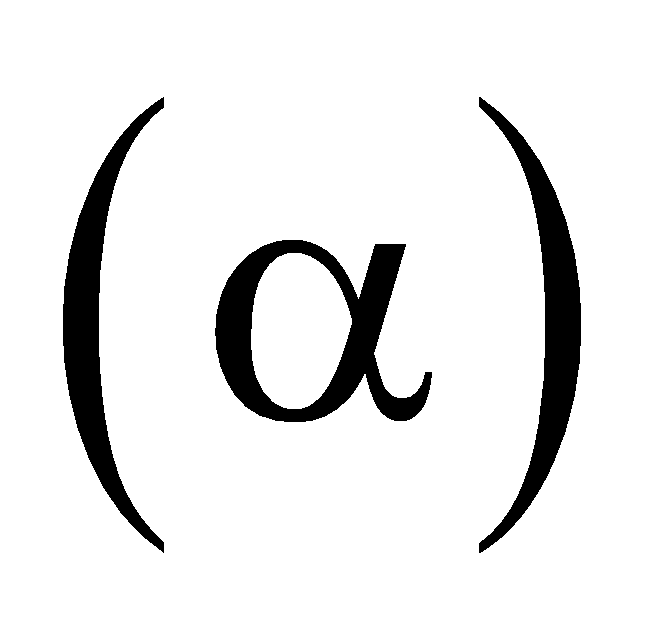qua hai điểm , và song song với 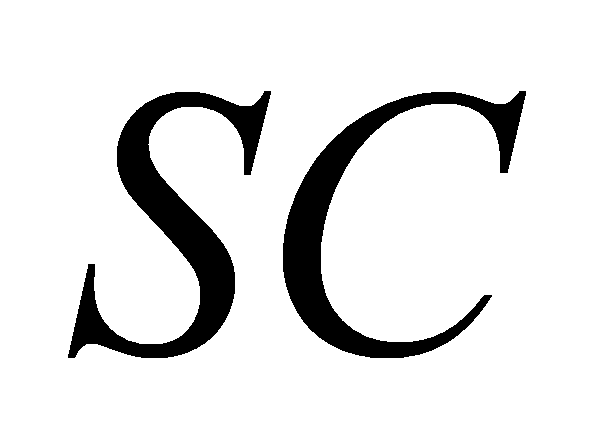chia khối chóp thành hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó ( số bé chia số lớn ).

• Cho khối lăng trụ

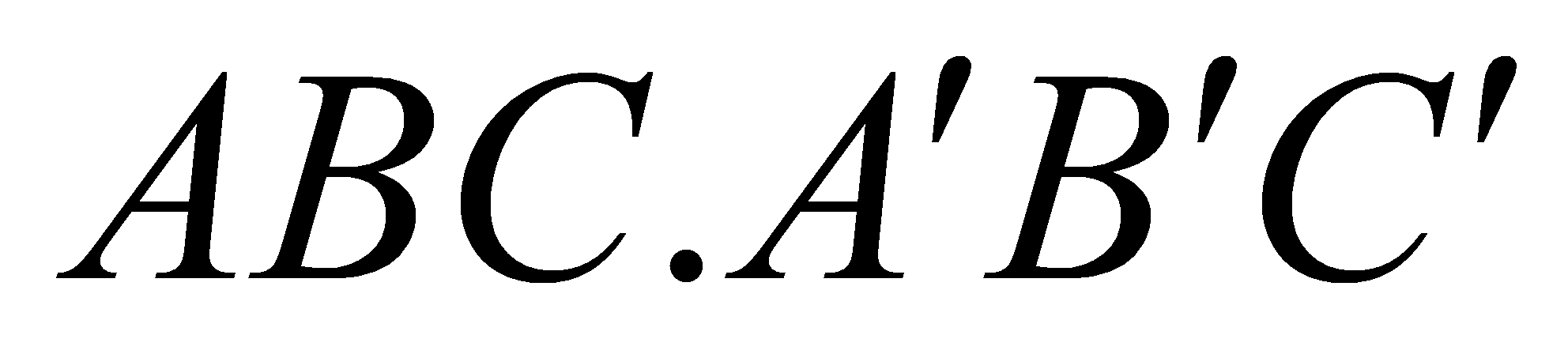  có thể tích bằng 2018. Gọi  là trung điểm ; 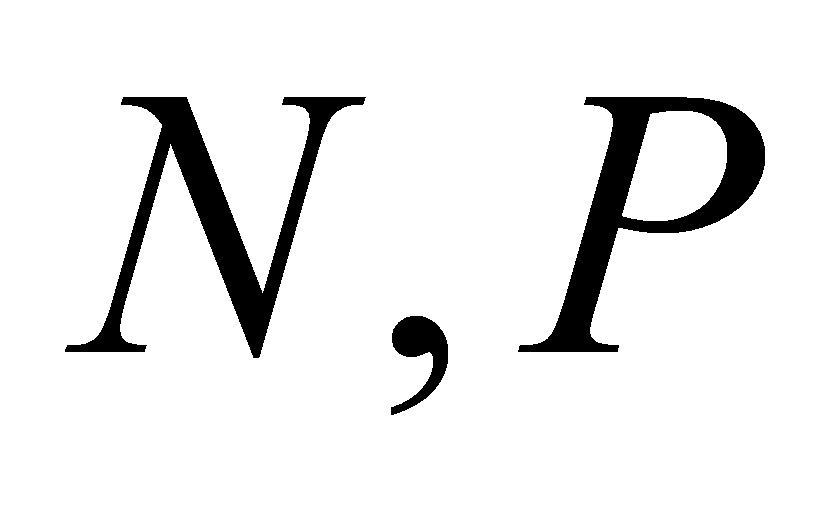lần lượt là các điểm nằm trên các cạnh 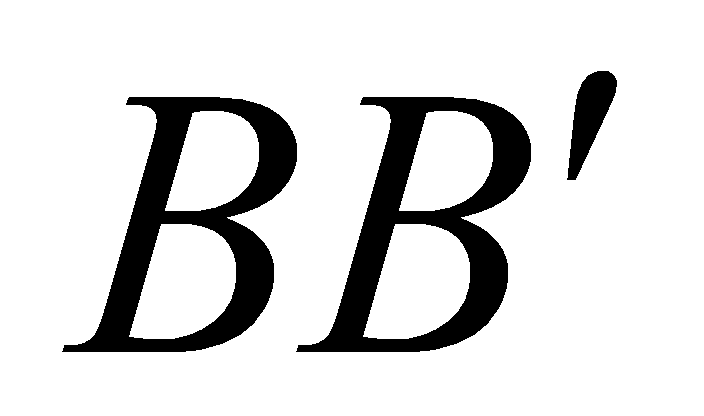, 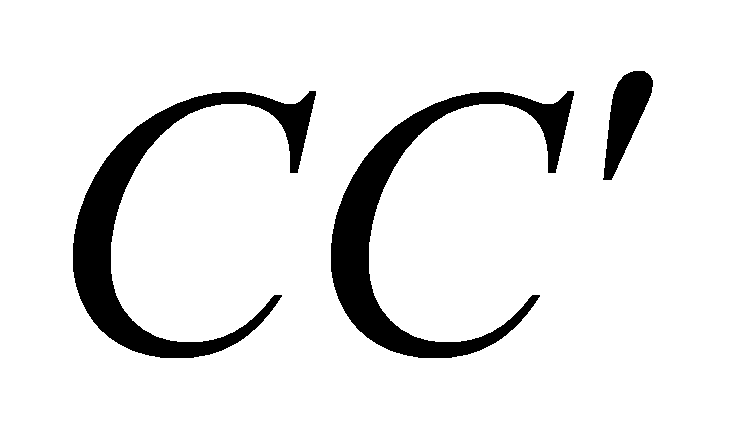sao cho 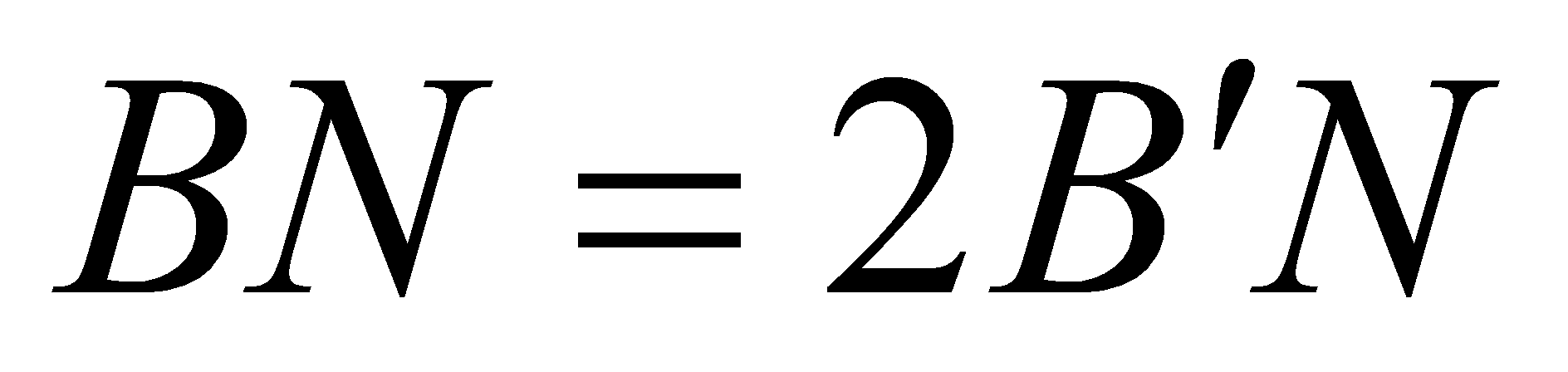, 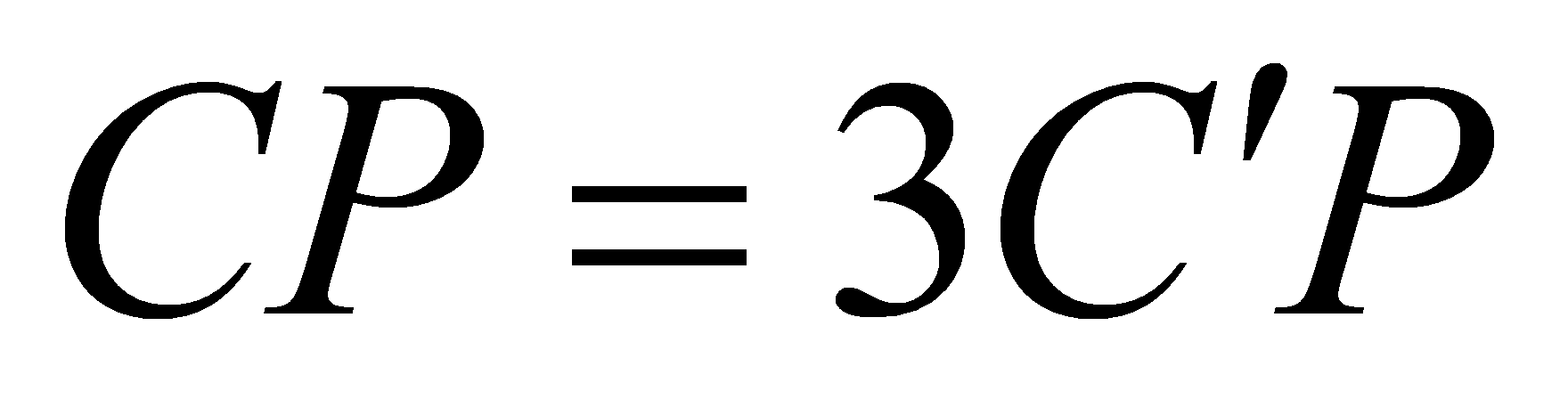. Tính thể tích khối đa diện .  

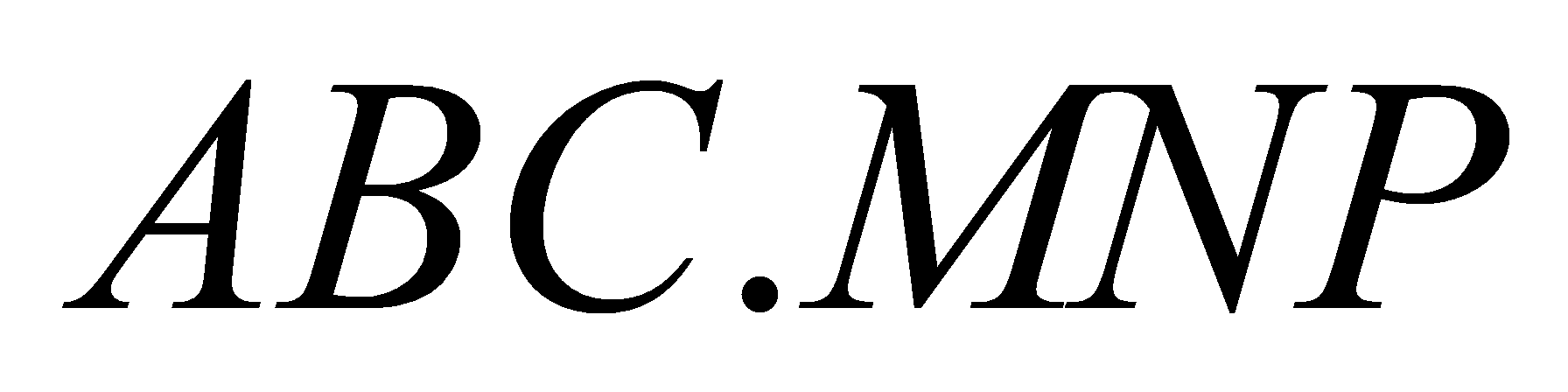• Cho tứ diện

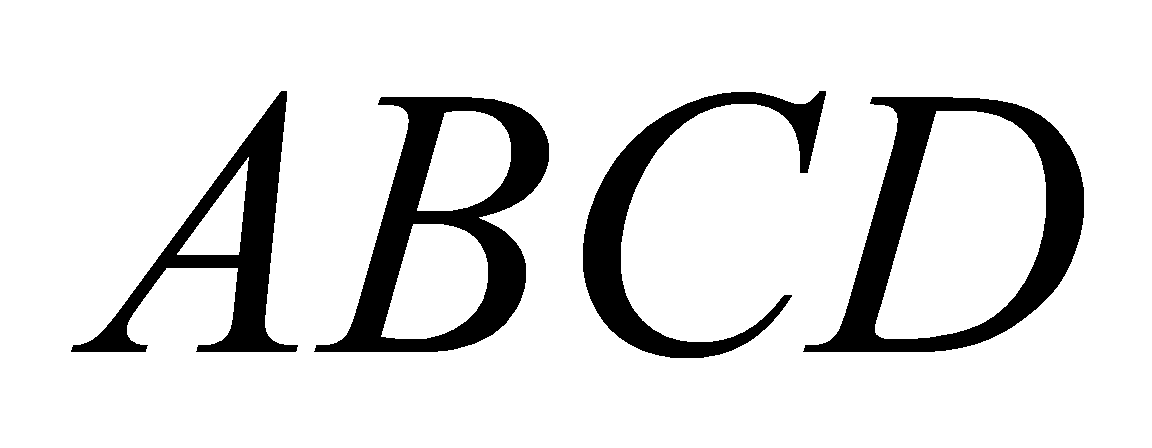  và 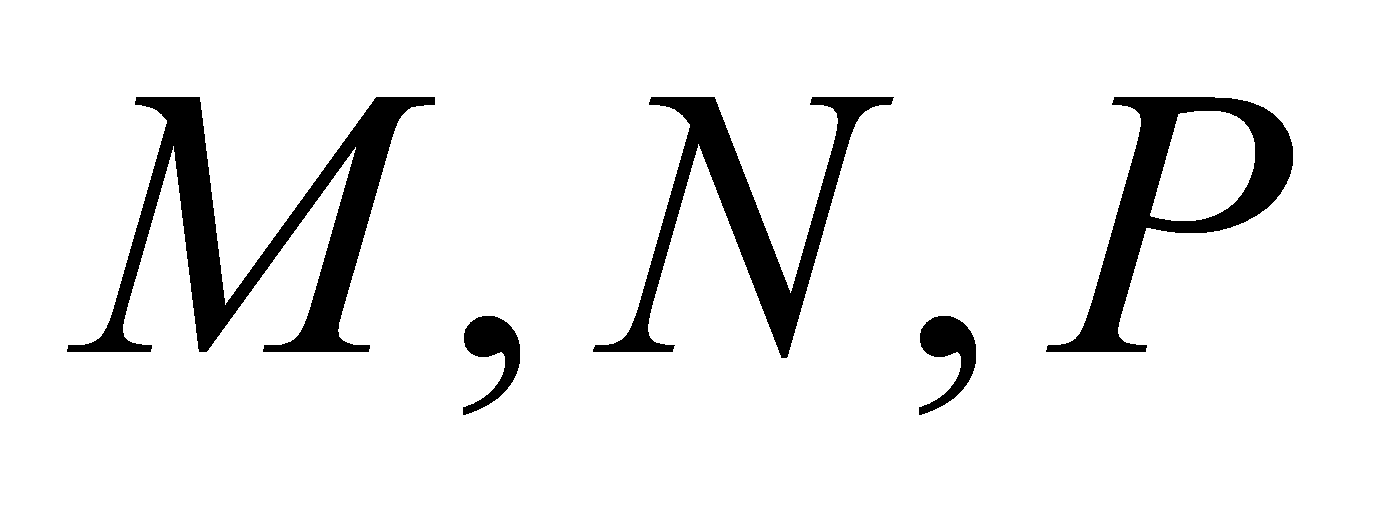lần lượt thuộc 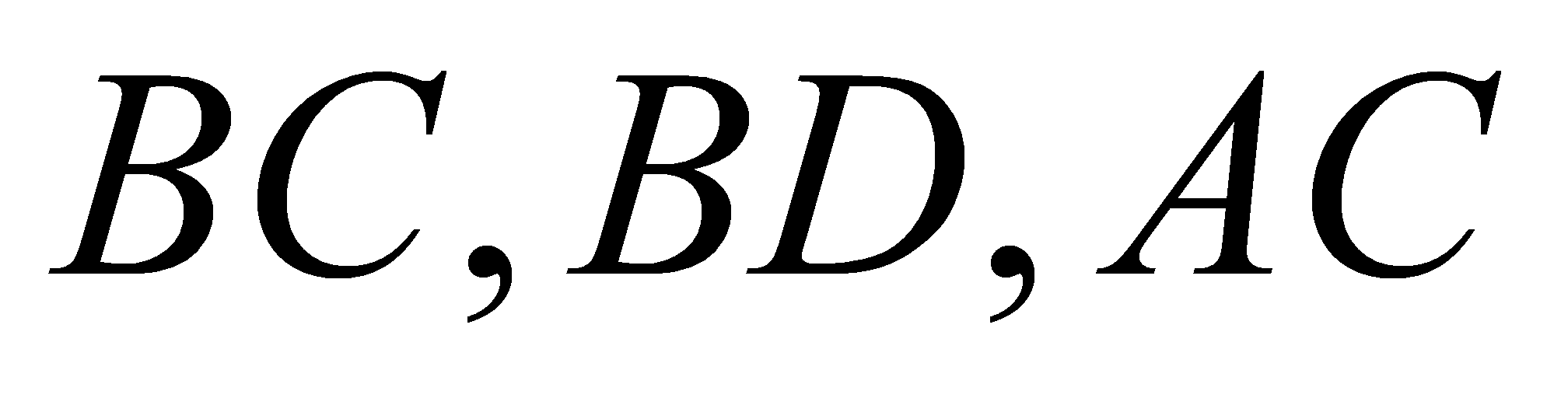sao cho 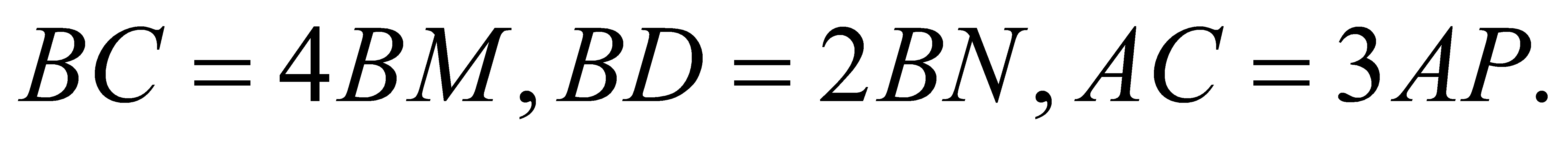Mặt phẳng cắt tại Q. Tính tỷ số thể tích hai phần khối tứ diện 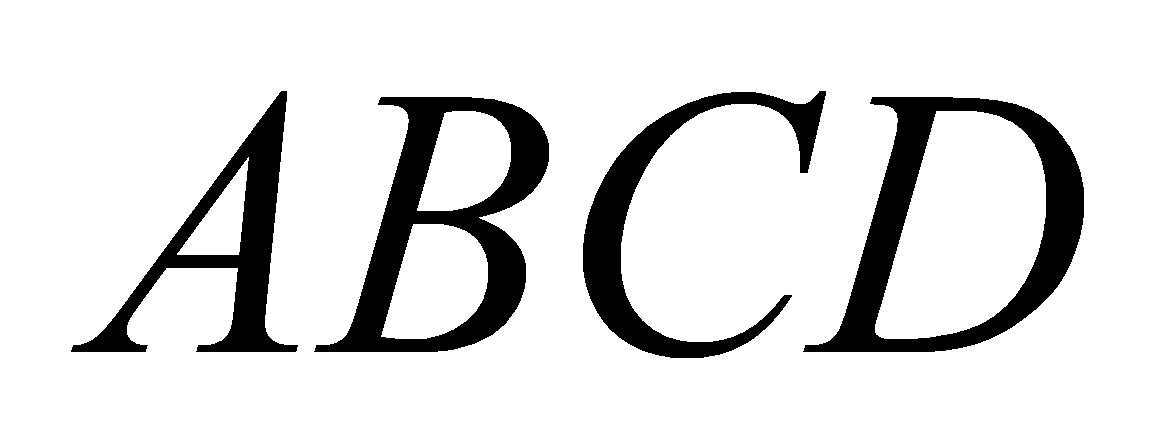bị chia bởi mặt phẳng

• Trong các câu sau đây, câu nào sai?         

• Cho hình chóp tam giác đều 

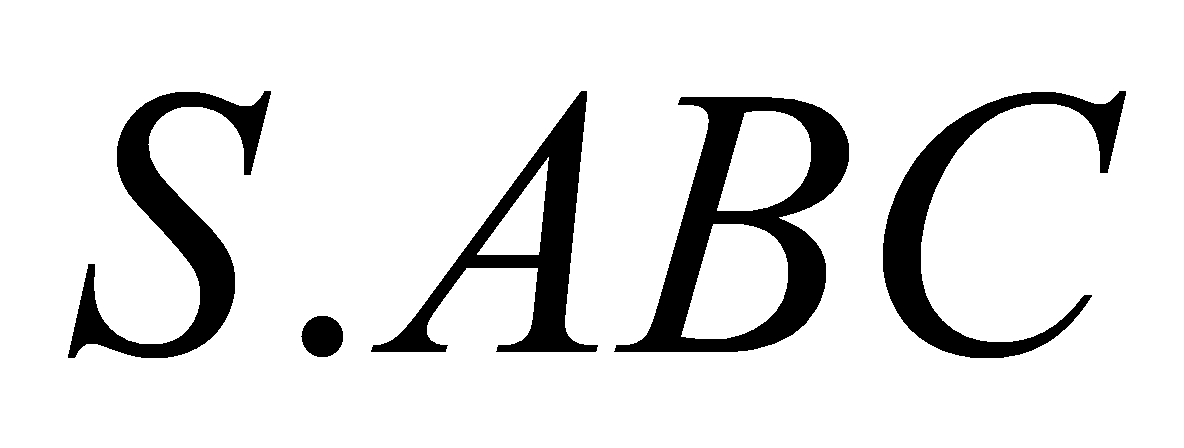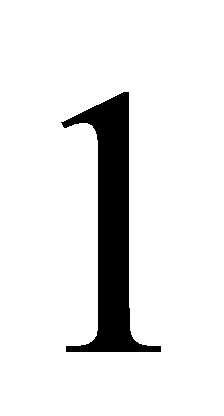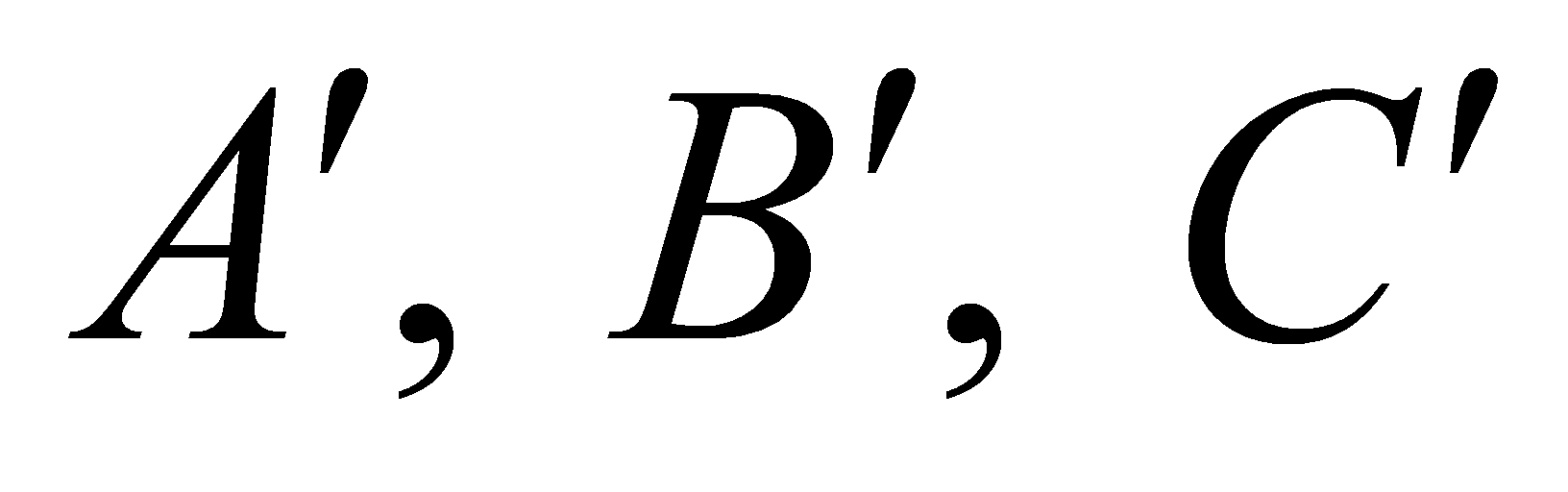   có cạnh đáy bằng , góc giữa cạnh bên và mặt đáy bằng Gọi lần lượt là các điểm đối xứng c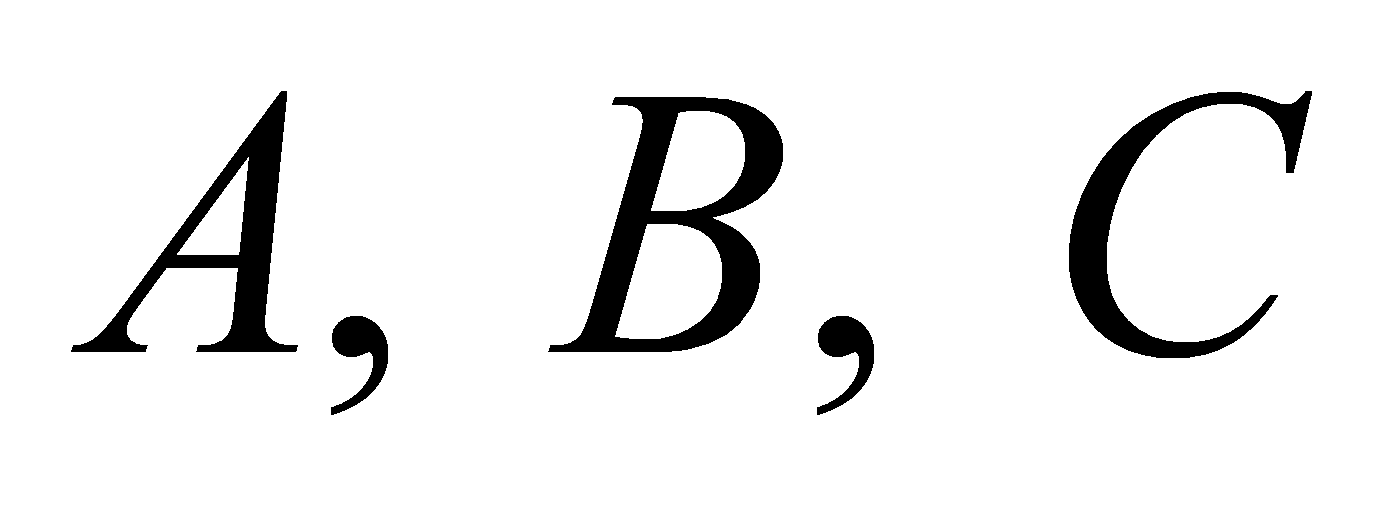ủa  qua . Thể tích của khối đa diện  bằng

• Cho hình chóp

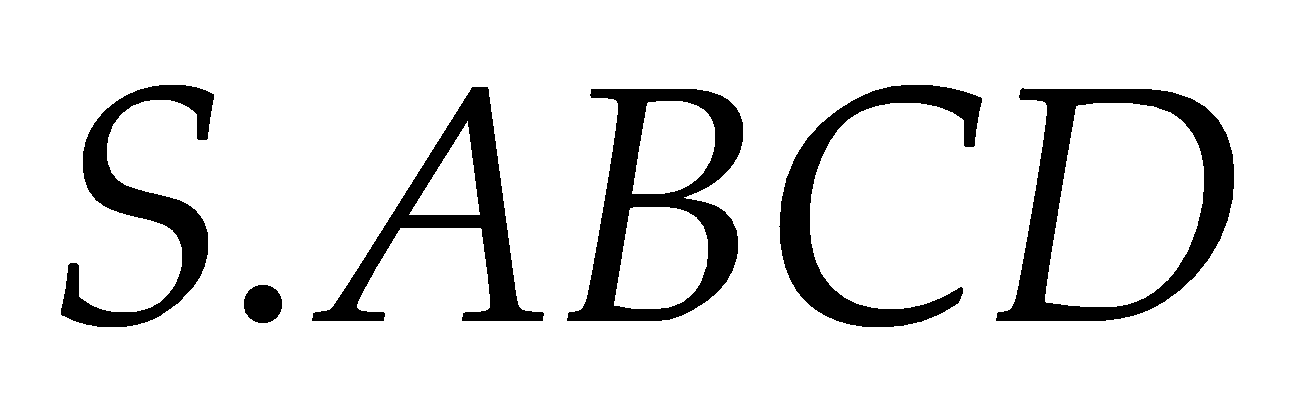  có đáy 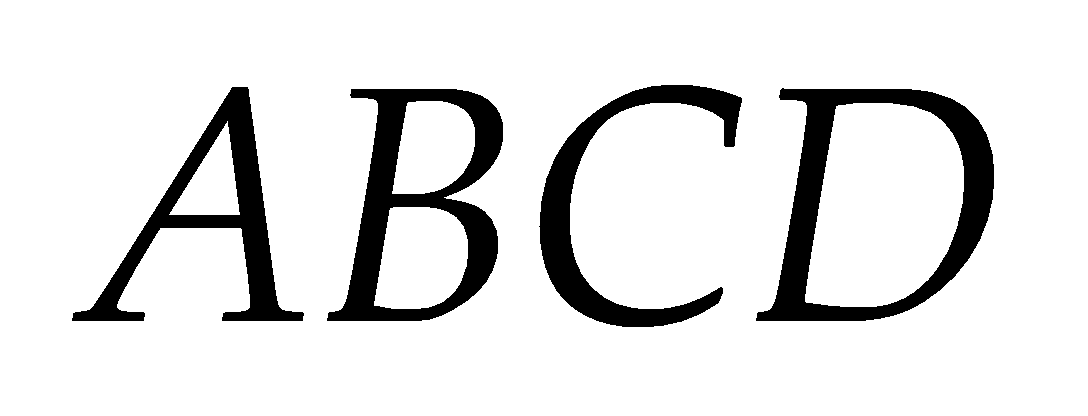là hình bình hành tâm . Xét các mệnh đề sau:

  (I) Khối chóp

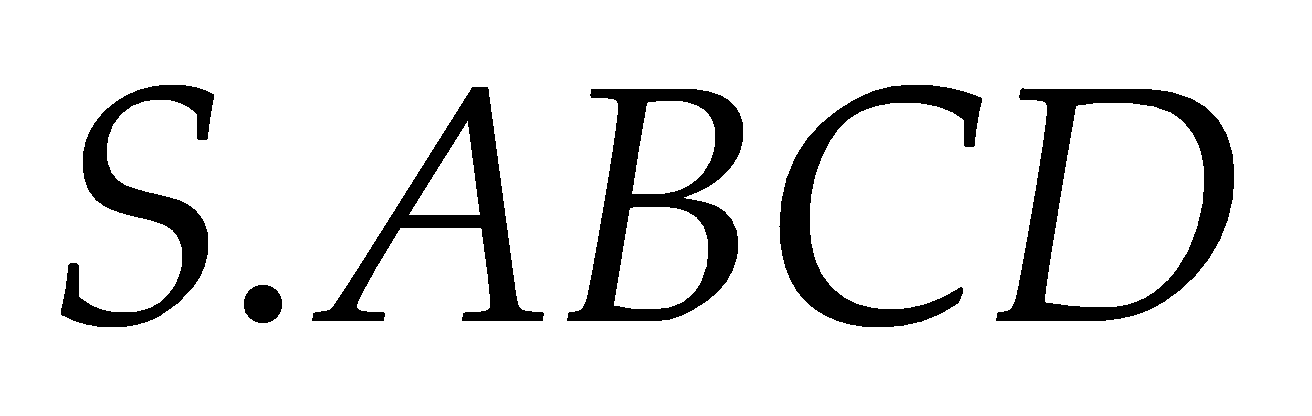  có thể phân chia thành bốn khối chóp , , , .

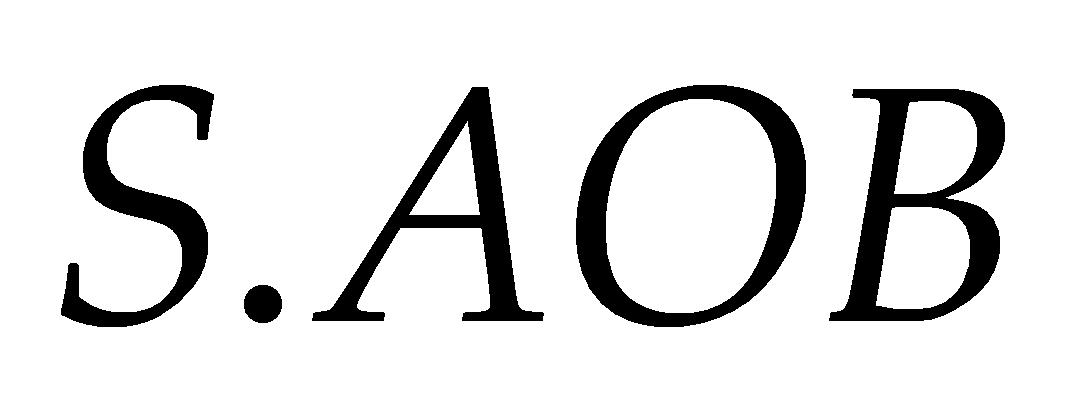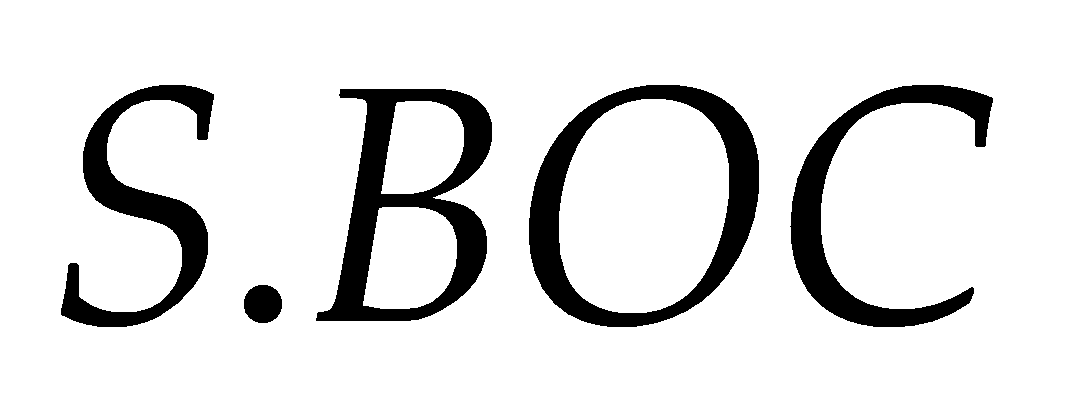  (II) Khối chóp

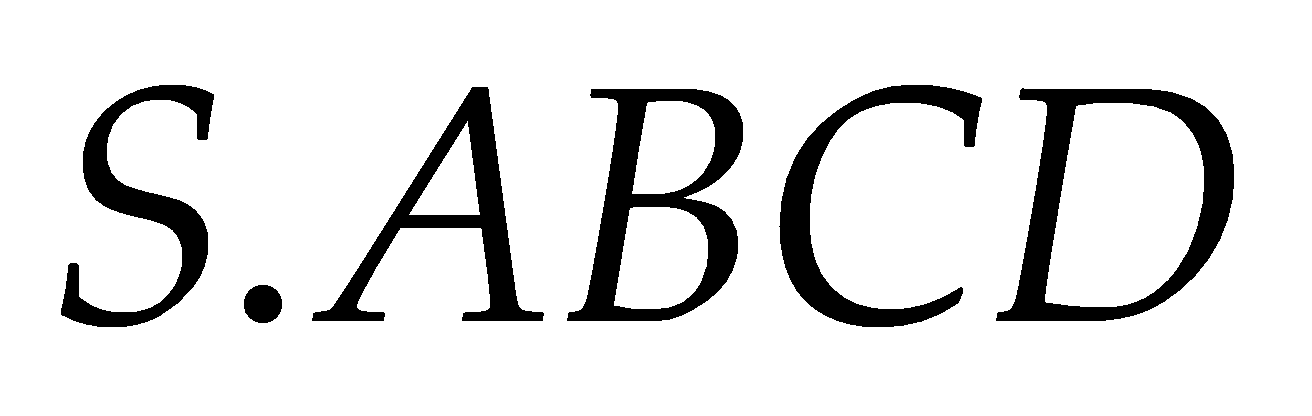  có thể phân chia thành hai khối chóp 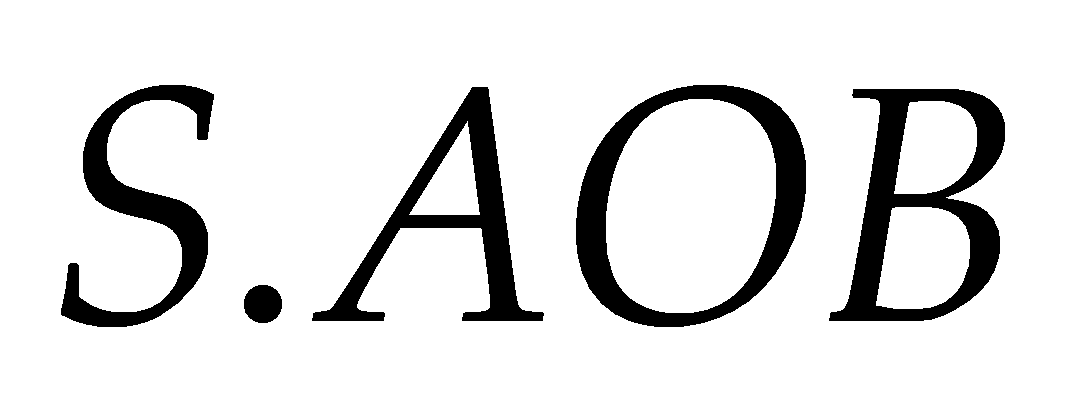và .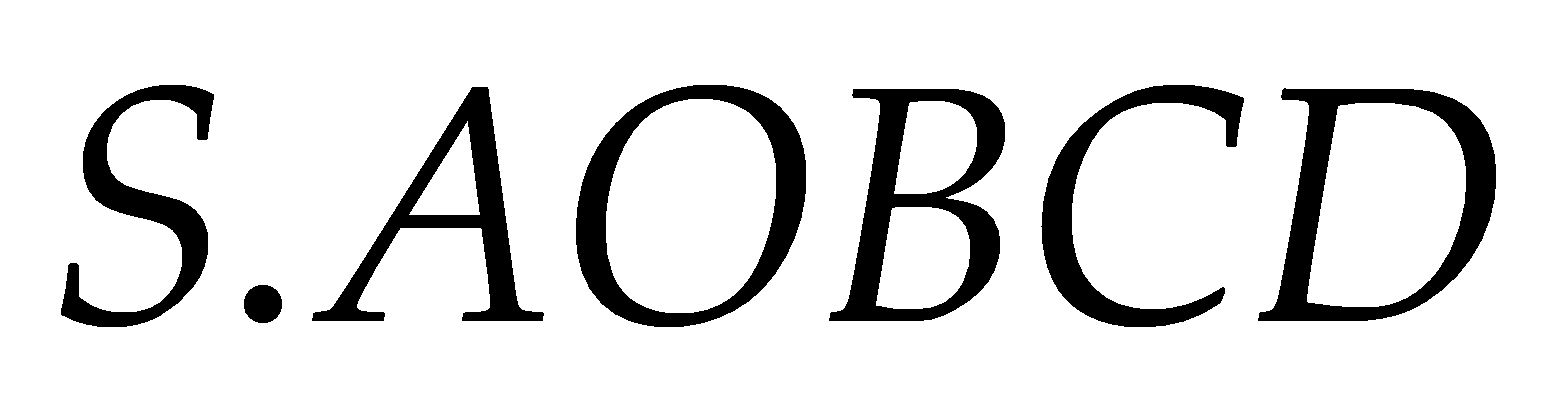

  Mệnh đề nào đúng?  

• Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt?

• Cho khối chóp

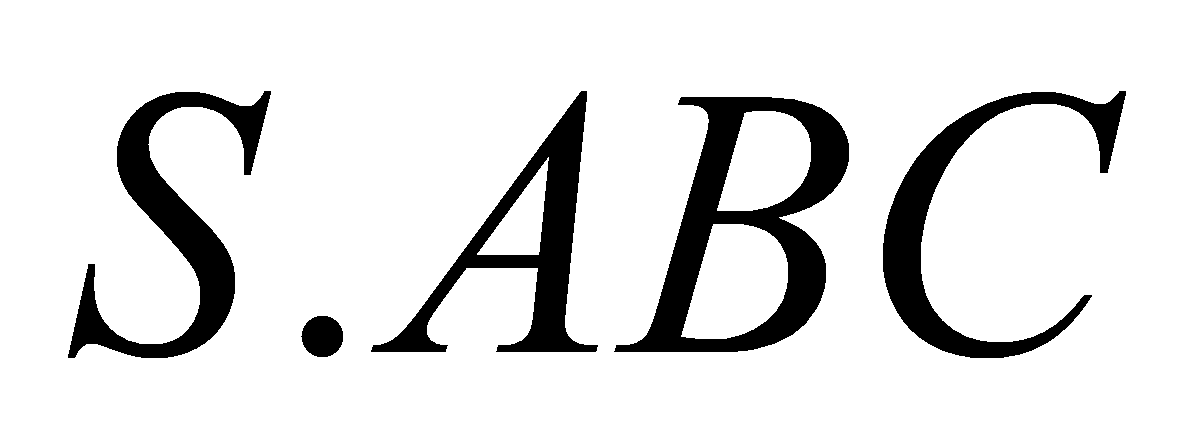  có , sao cho 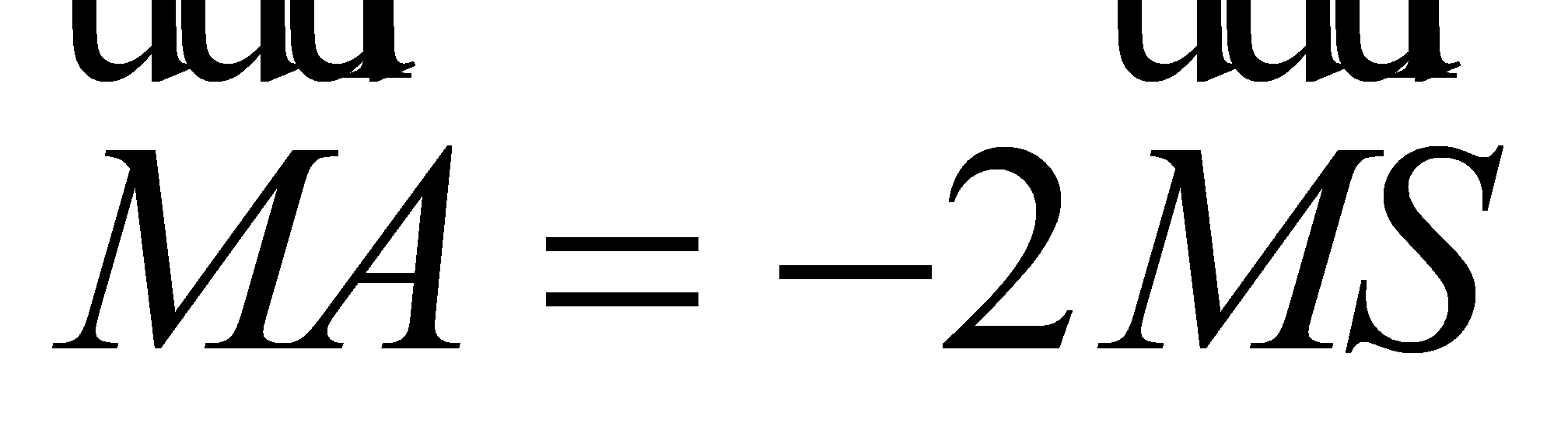, 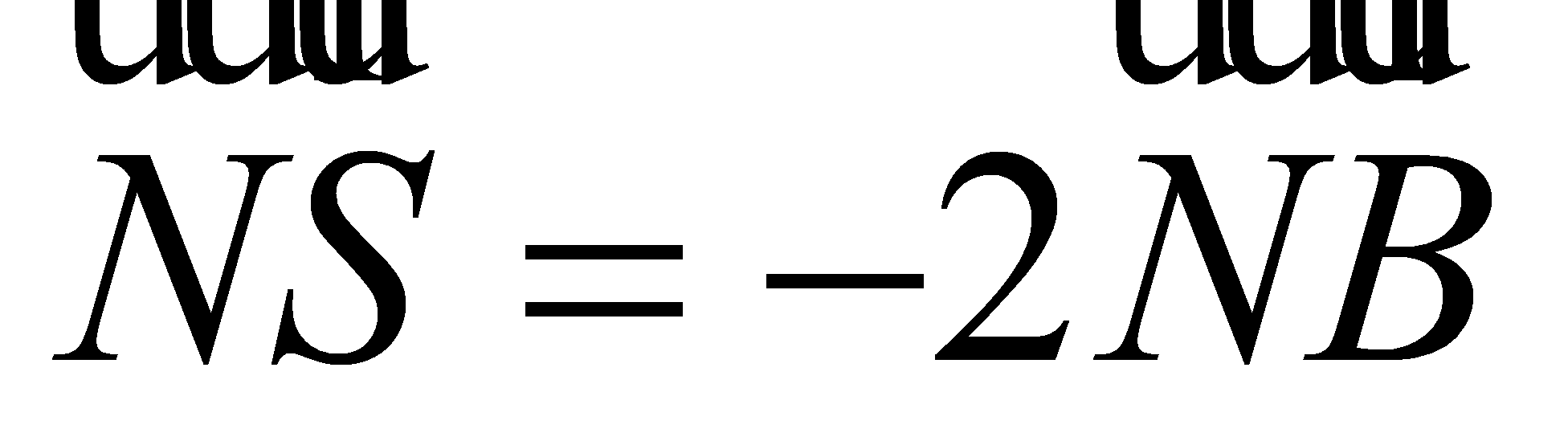. Mặt phẳng 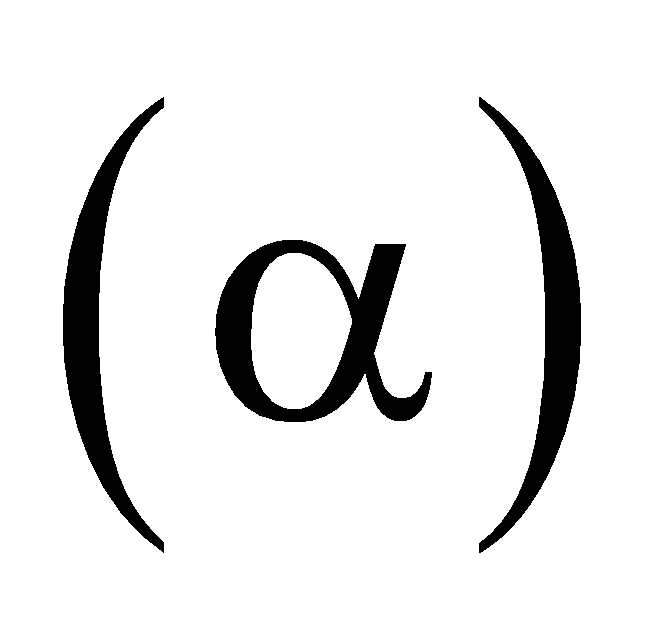qua hai điểm , và song song với 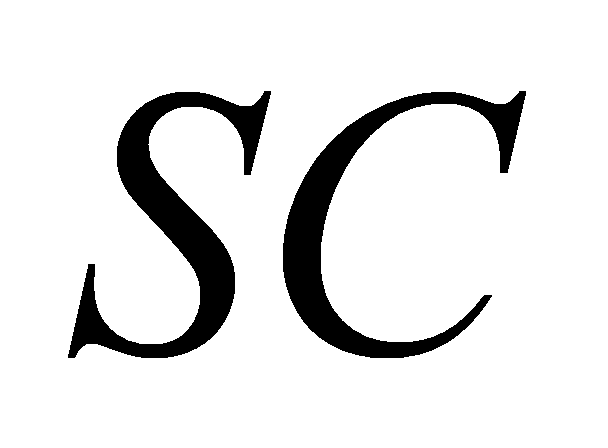chia khối chóp thành hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó ( số bé chia số lớn ).

• Cho khối đa diện. Trong các mệnh đề sau, mệnh đề nào sai?  

• Cho hình lăng trụ tam giác đều

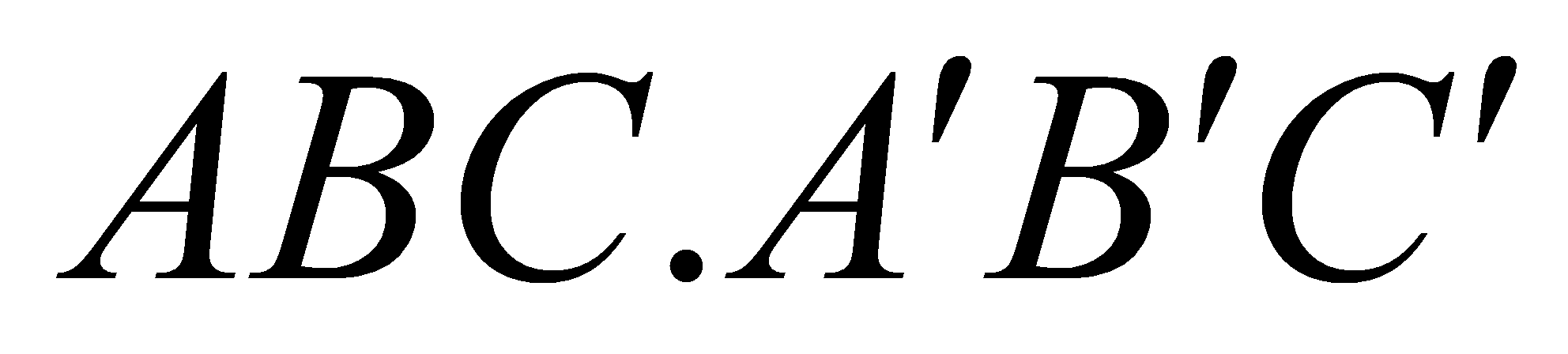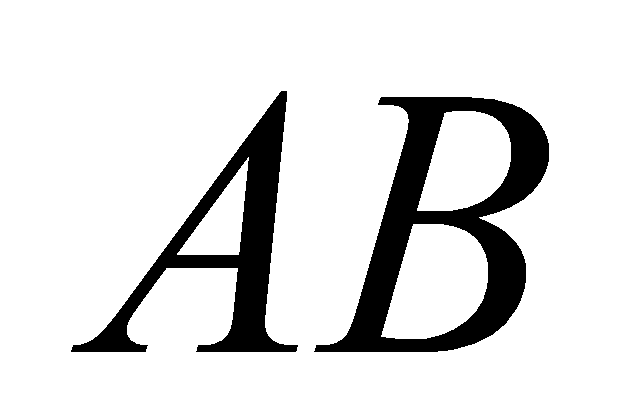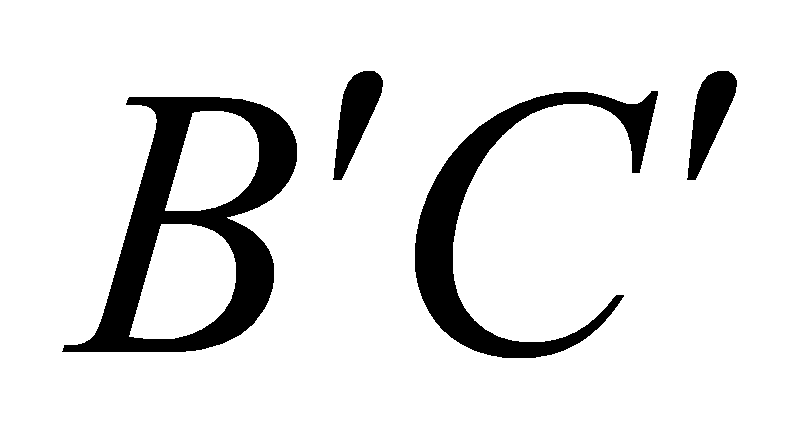  có tất cả các cạnh bằng . Gọi ,  lần lượt là trung điểm của các cạnh và . Mặt phẳng 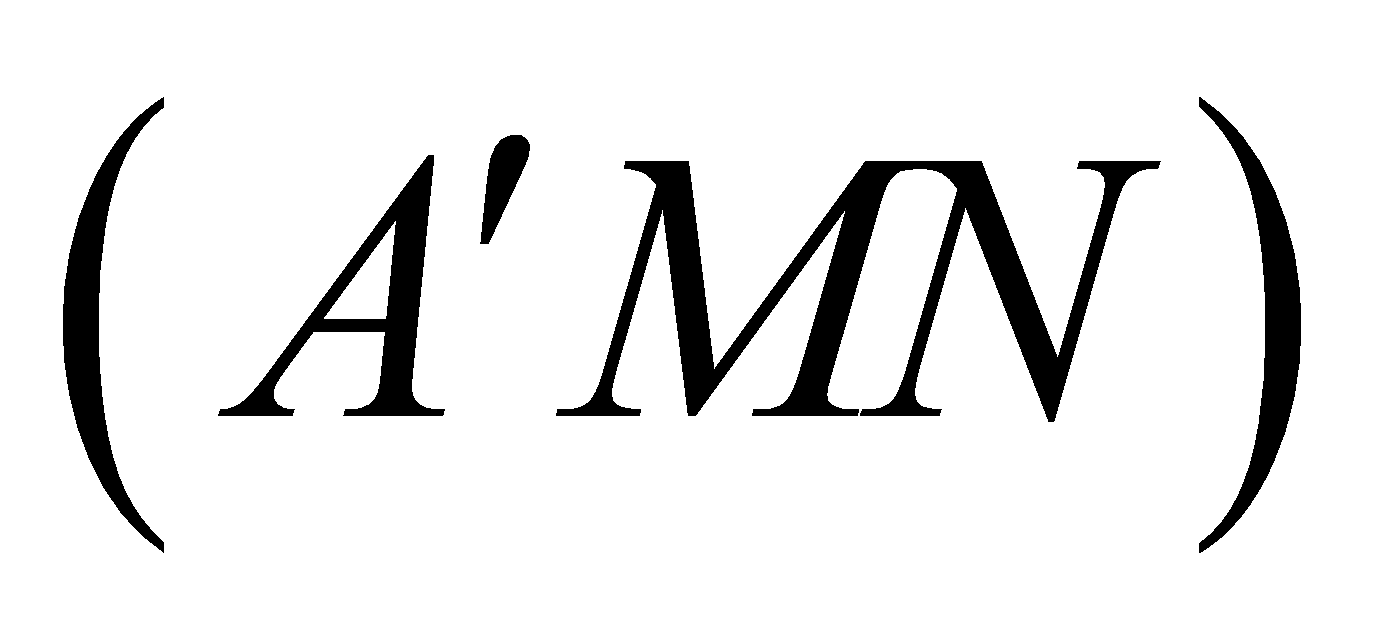cắt cạnh 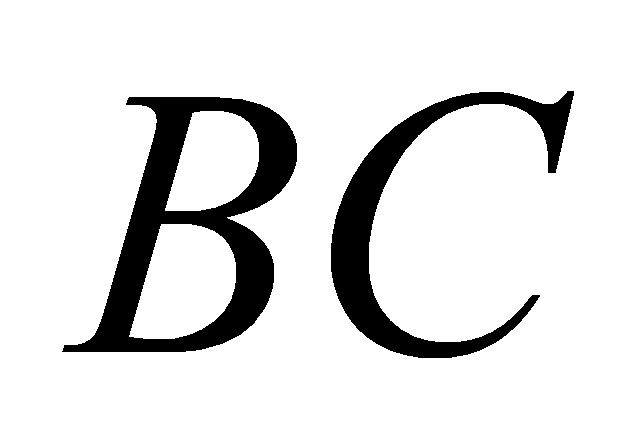tại . Tính thể tích khối đa diện .  

• Vật thể nào dưới đây không phải là khối đa diện?

• Cho hai đường thẳng (d) và (d’) cắt nhau. Có bao nhiêu phép đối xứng qua mặt phẳng biến (d) thành (d’)?                

• Cho khối lập phương

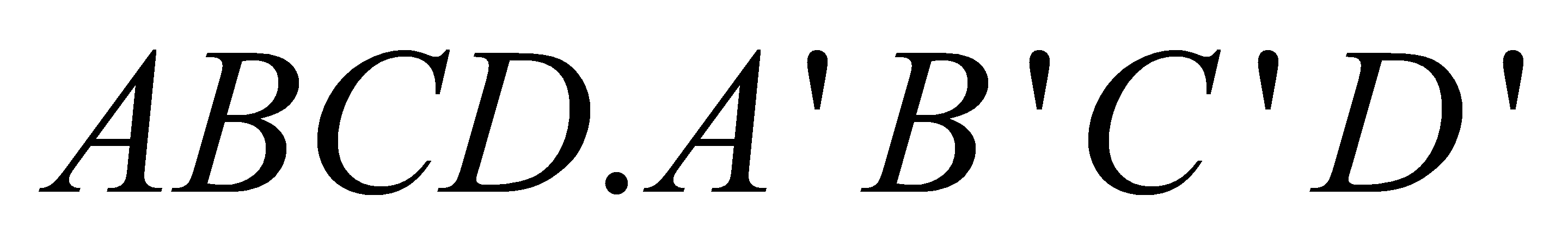  . Mặt phẳng 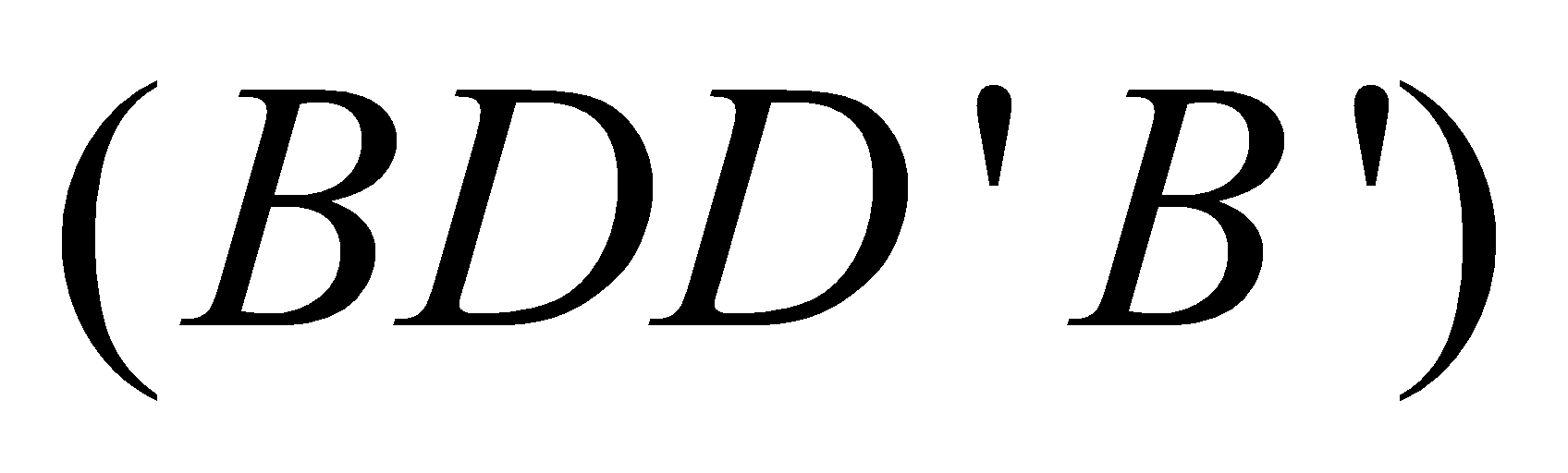chia khối lập phương thành

• Cho khối chóp

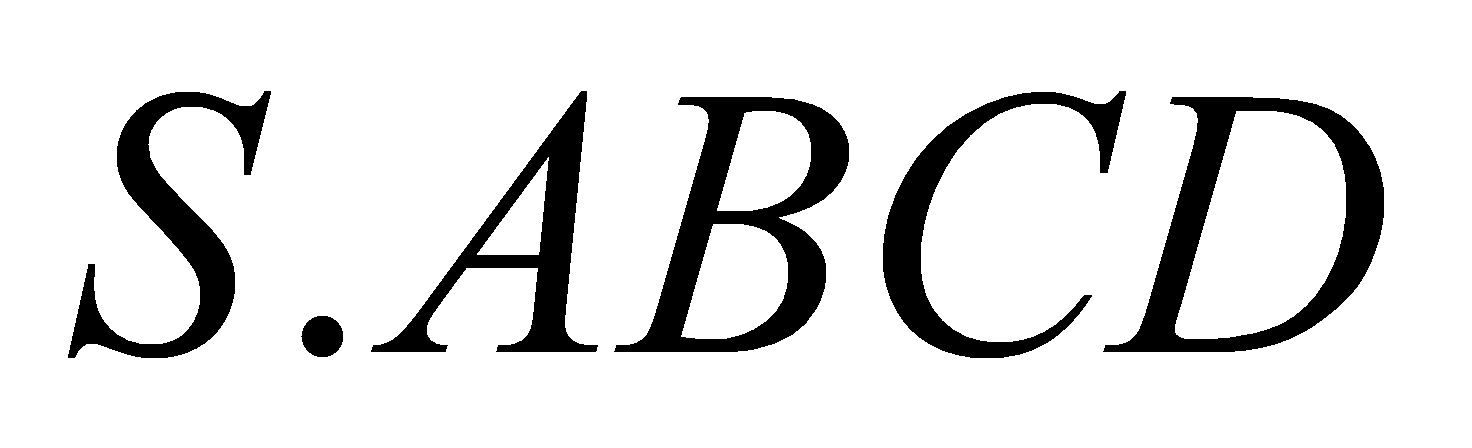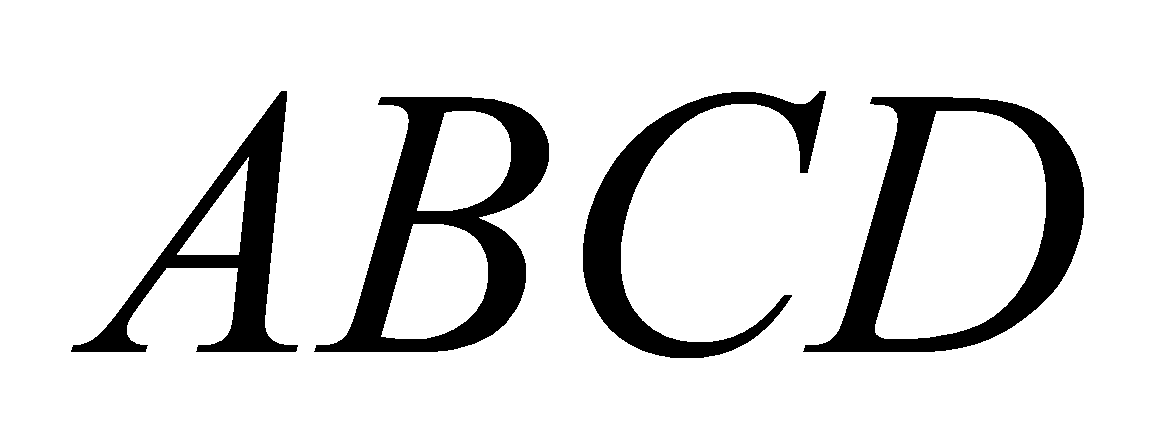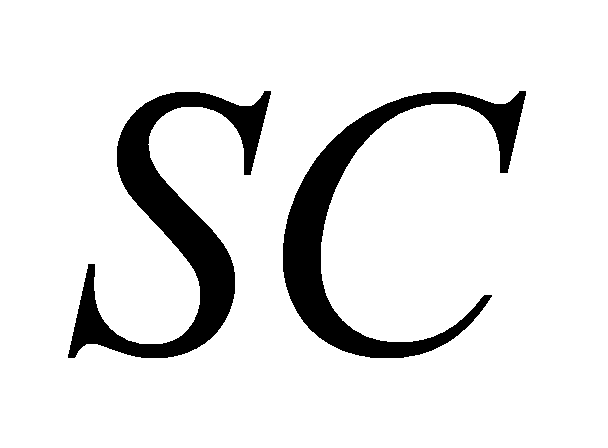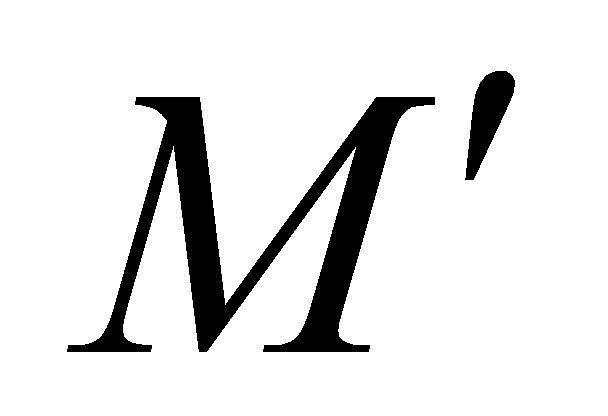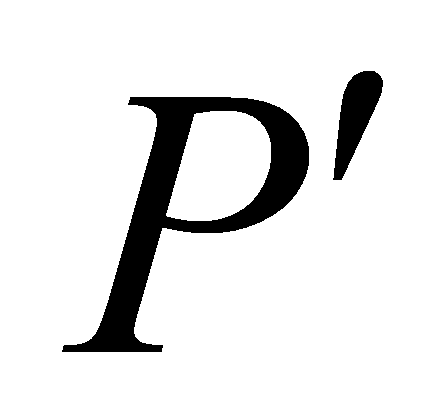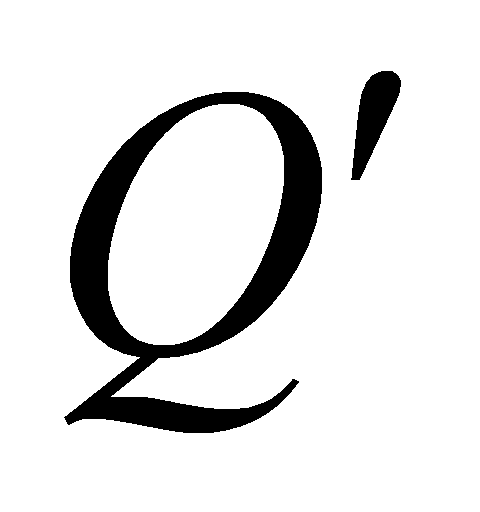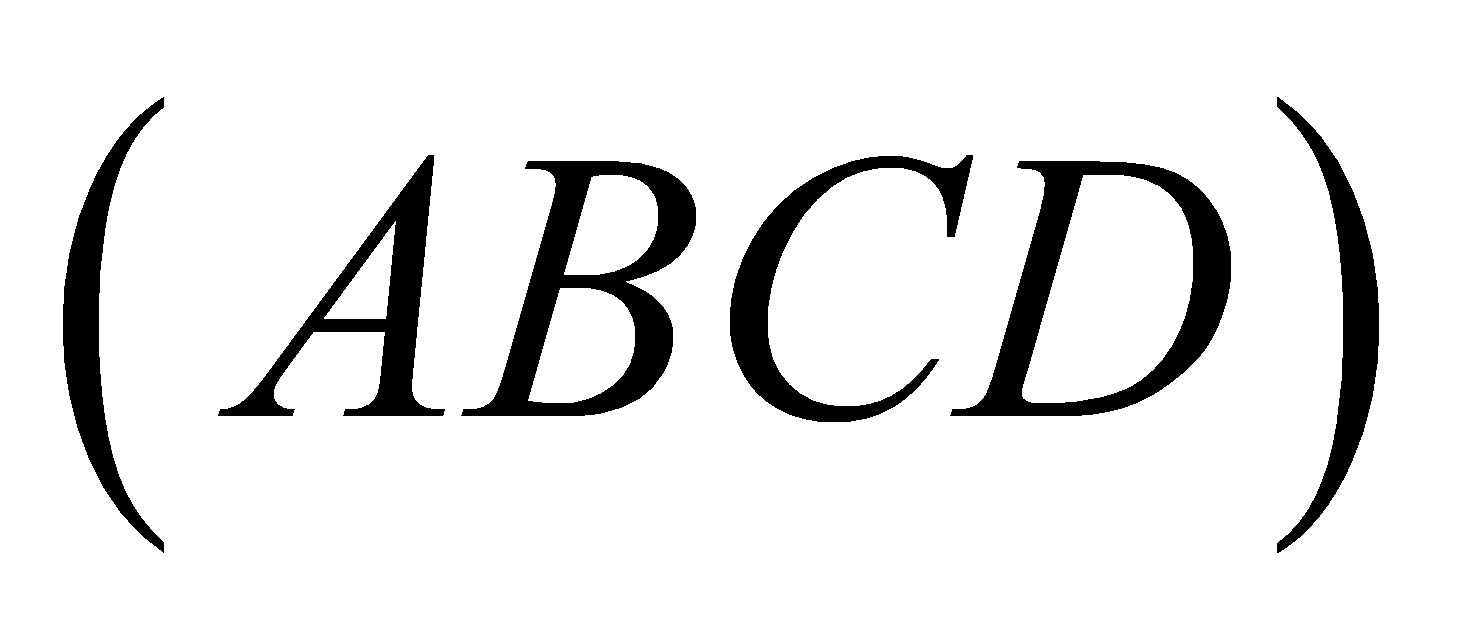  có đáy là hình chữ nhật. Một mặt phẳng thay đổi nhưng luôn song song với đáy và cắt các cạnh bên , , , lần lượt tại , , , . Gọi , , , lần lượt là hình chiếu vuông góc của , , , lên mặt phẳng . Tính tỉ số để thể tích khối đa diện 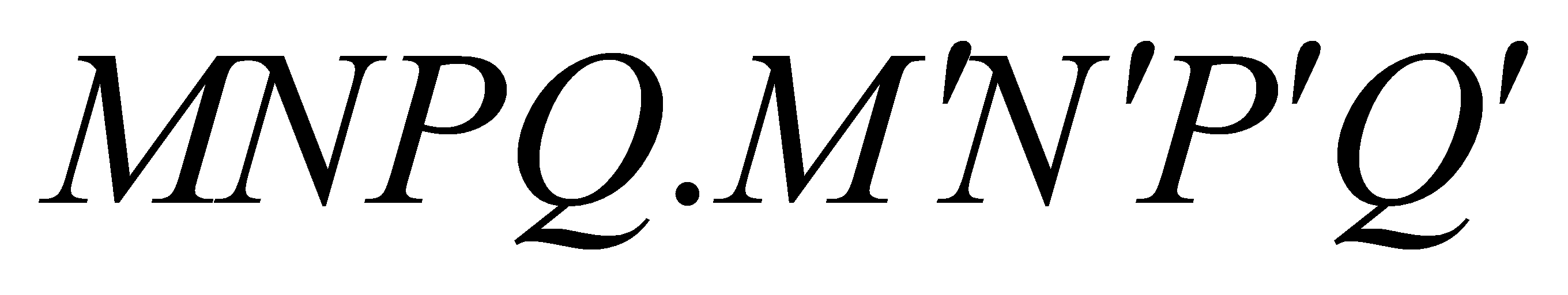đạt giá trị lớn nhất.

• Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất

• Cho khối chóp tứ giác đều S.ABCD. Gọi M là trung điểm SC, mặt phẳng (P) chứa AM và song song với BD chia khối chóp thành 2 khối đa diện. Đặt 

   là thể tích khối đa diện có chứa đỉnh S và  là thể tích khối đa diện có chứa đáy. Tỉ số  bằng:         

• Một hình hộp chữ nhật (không phải hình lập phương) có bao nhiêu mặt phẳng đối xứng?  

• Cho một khối chóp có đáy là đa giác lồi

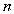   cạnh. Trong các mệnh đề sau đây, mệnh đề nào đúng:        

• Cho hình chớp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng

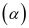   đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số  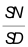để 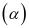 chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau

• Trong các mệnh đề sau, mệnh đề nào đúng? Số các đỉnh, hoặc các mặt của bất kỳ hình đa diện luôn  

• Cắt khối trụ

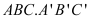   bởi các mặt phẳng  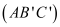và 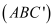 ta được những khối đa diện nào?

• Số cạnh bên n của một lăng trụ luôn luôn là:  

• Trong không gian cho hai tam giác ABC và A’B’C’ bằng nhau (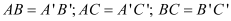 ). Chọn mệnh đề đúng trong các mệnh đề sau  

• Cho khối chóp 

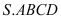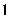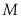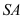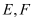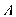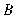   có đáy là hình bình hành, thể tích bằng . Gọi  là trung điểm cạnh; các điểm  lần lượt là điểm đối xứng của  qua  và 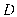. Mặt phẳng  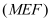cắt các cạnh  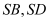lần lượt tại các điểm 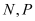. Thể tích của khối đa diện  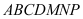bằng  

• Vật thể nào dưới đây không phải là khối đa diện?
  

• Cho hình chóp tứ giác đều S.ABCD. Nhận định nào sau đây là sai?         

• Số hình đa diện lồi trong các hình dưới đây là                

   

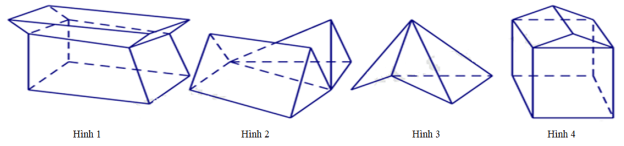
• Cho khối lăng trụ

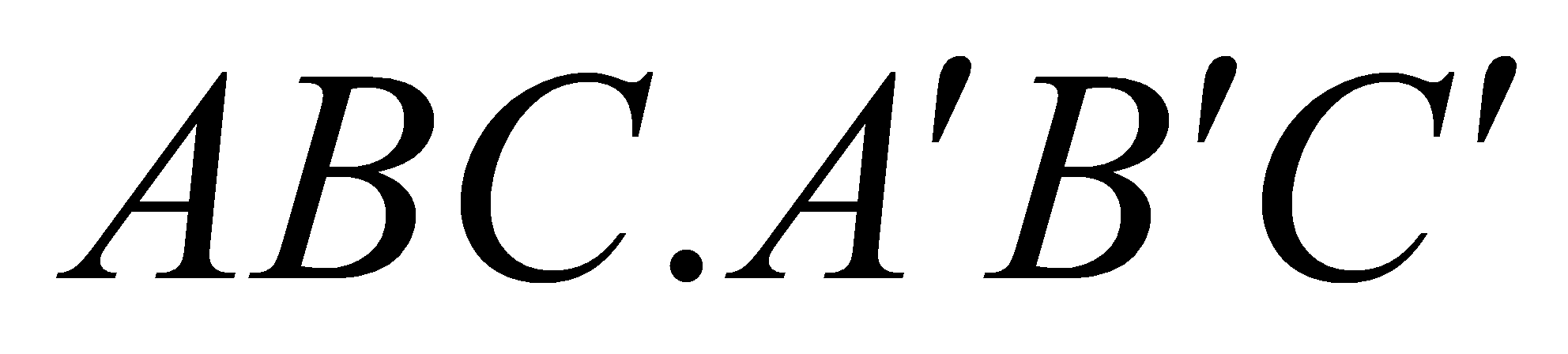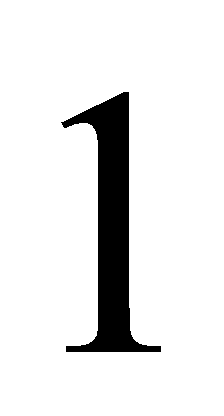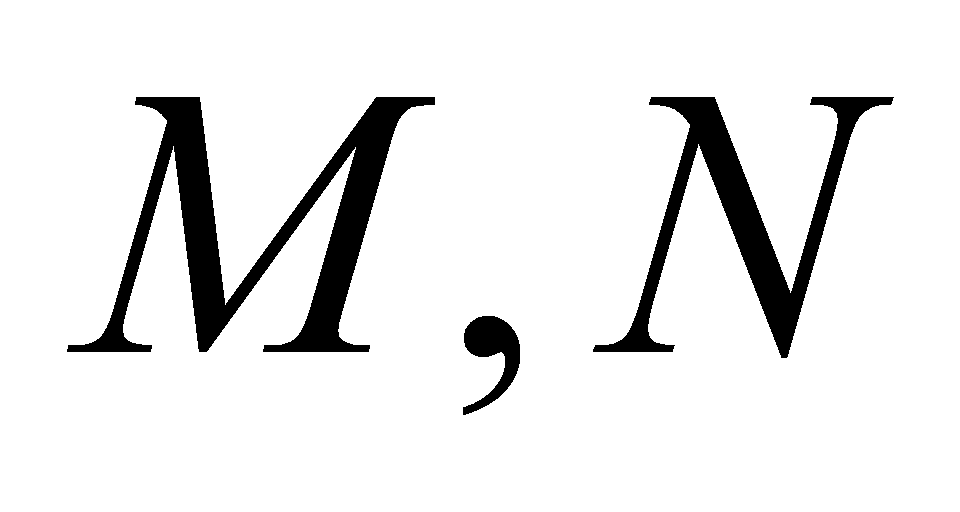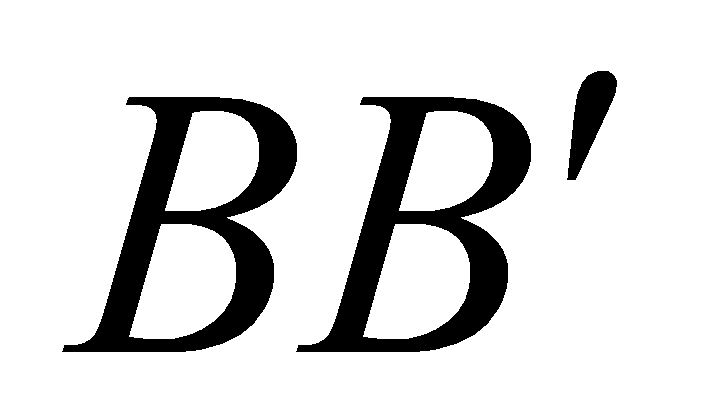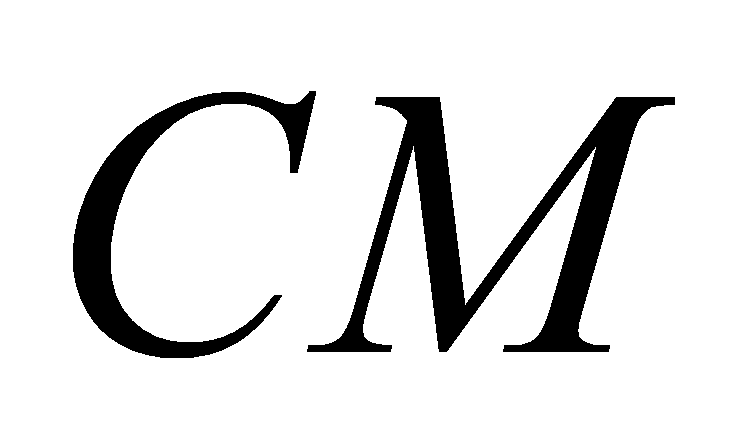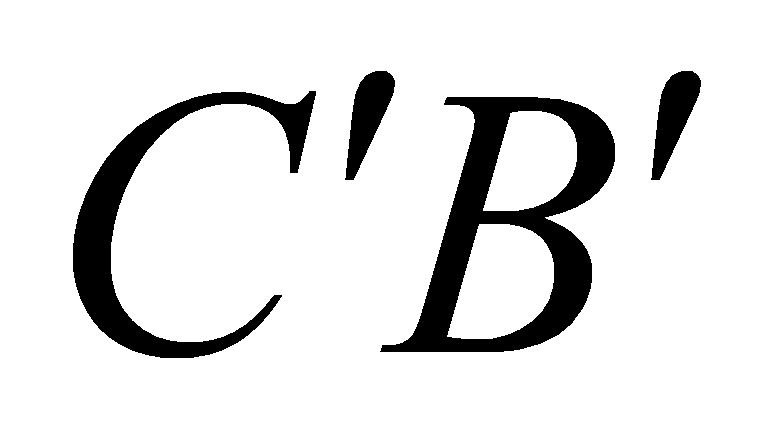  có thể tích bằng . Gọi lần lượt là trung điểm của các đoạn thẳng  và . Đường thẳng cắt đường thẳng  tại , đường thẳng cắt đường thẳng tại . Thể tích khối đa diện lồi bằng

• Cho hình lập phương 

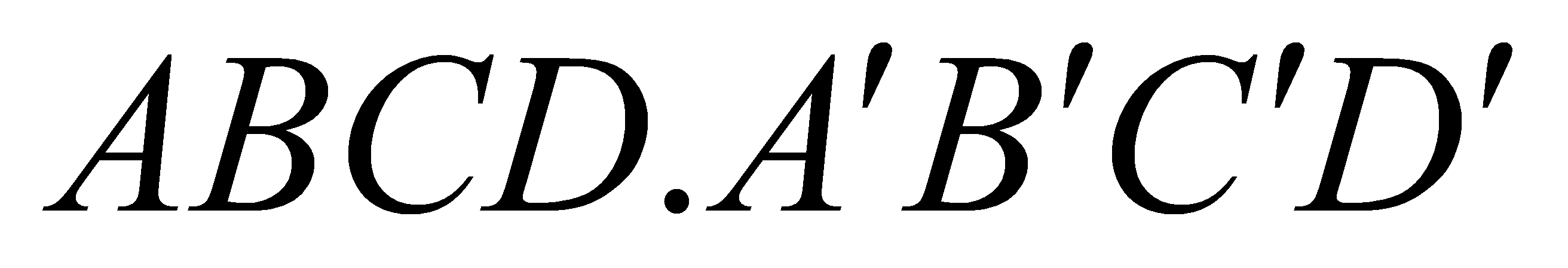   cạnh . Gọi  là trung điểm của 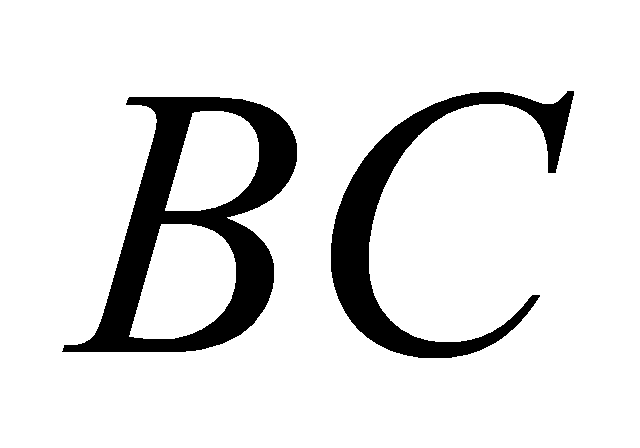,  thuộc cạnh  thỏa 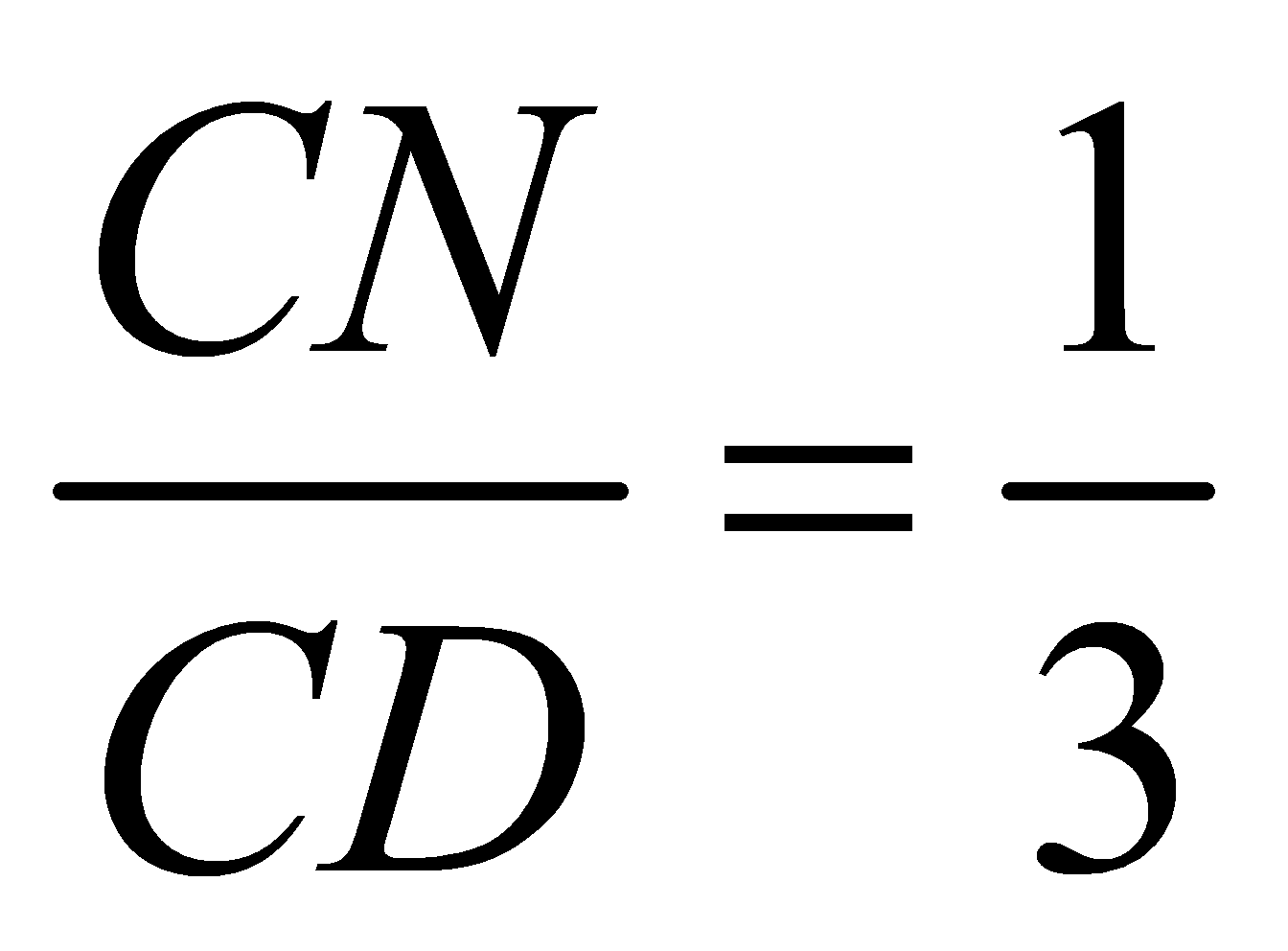. Mặt phẳng  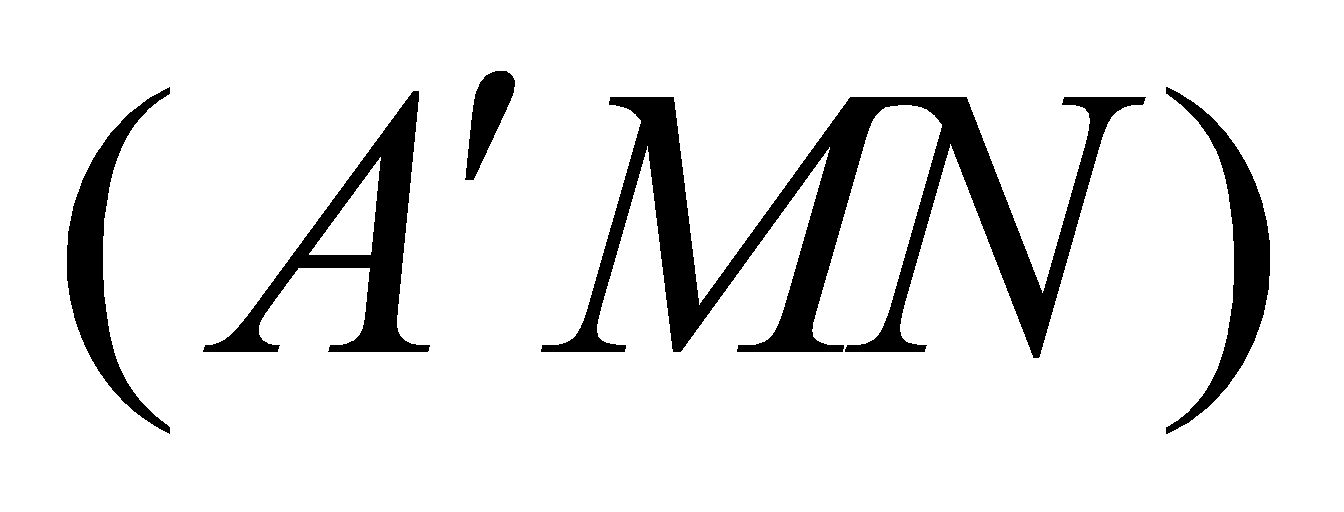chia khối lập phương thành hai khối, gọi  là khối chứa điểm . Thể tích của khối  theo là?

• Cho hình chóp

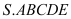   có đáy là hình ngũ giác và có thể tích là 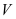. Nếu tăng chiều cao của chóp lên  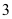lần đồng thời giảm độ dài cạnh đáy đi  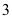lần ta được khối chóp mới  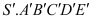có thể tích 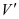. Tỉ số  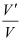là

• Cho hình chóp 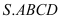 có đáy là hình bình hành và thể tích 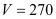. Lấy điểm  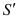trong không gian thỏa mãn 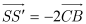. Tính thể tích  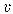của phần chung của hai khối chóp  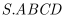và 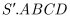. (tham khảo hình vẽ sau)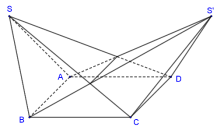    

• Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất

Một số câu hỏi khác có thể bạn quan tâm.

• Đặc điểm nào sau đây không phải của vật chất sống?

• Điều nào sau đây đúng khi nói về tế bào?

• Tập hợp các cá thể cùng loài, cùng sống trong một khoảng không gian xác định ở một thời điểm xác định có quan hệ sinh sản với nhau được gọi là

• Điểm giống nhau về cấu tạo của prôtêin và axit nuclêic là

• Tập hợp các cơ quan bộ phận của cơ thể cùng thực hiện một chức năng được gọi là

• Ở sinh vật, đơn vị quần xã dùng để chỉ tập hợp của

• Một hệ thống hoàn chỉnh và tương đối ổn định bao gồm quần xã sinh vật và môi trường sống của nó được gọi là

  Cho 2 đường thẳng cắt nhau d và d có bao nhiêu phép đối xứng tầm?

  Hai đường thẳng d và d′ cắt nhau thì có hai phép đối xứng trục biến đường thẳng này thành đường thẳng kia, đó là hai phép đối xứng trục với trục là hai đường phân giác có góc tạo bởi hai đường thẳng d và d′ .

  Có bao nhiêu phép đối xứng trục biến đường thẳng d thành chính nó?

  Có vô số phép. Lời giải. Gọi là đường thẳng vuông góc với đường thẳng . d Khi đó, phép đối xứng trục biến d thành chính nó.

  2 đường thẳng song song có bao nhiêu trục đối xứng?

  1) Nếu các đường thẳng giao nhau thì có 2 trục đối xứng; nếu chúng song song với nhau thì có vô số trục đối xứng.
  

programming
bao nhiêu